BGW
在前面的 GMW 中, 我們看到在 boolean circuit 上, 用 XOR 做 additive sharing 拆分的作法.
接下來要介紹的 BGW, 是在 1988 由 Ben-Or / Goldwasser / Wigderson 三人所提出的.
BGW 使用由 + 和 * 所組成的 arithmetic circuit.
BGW 使用由多項式拆分的 Shamir’s secret sharing.
BGW 不用 oblivious transfer.
(Shamir’s secret sharing 請先看這篇)
從最外面看, “拆分 input 成 shares / 逐 gate 計算新 shares / 合併 output shares” 的三大步驟還是一樣的. 我們直接聚焦在如何逐 gate 計算新的 shares.
”+” Gate
先看比較簡單的 “+” gate. 假設 gate 的三條 wire 的關係是 u + v = w .
現有 A B C 三個 party 來到了 “+” gate 前. 三人手上共同持有著 [u] = (u1, u2, u3) 和 [v] = (v1, v2, v3). 我們希望經過計算後, 他們手上能有 [u+v] .
根據 Shamir’s secert sharing 的性質, 這步不用互相溝通. 直接各自計算出 (u1+v1, u2+v2, u3+v3) 就好了. [link]
“*” Gate
複雜的地方在 “*” gate.
我們有 3 個 party. 3 點最高可以決定 2 次曲線. 但平常的 shares 我們不能用 2 次曲線產生, 必須保持在 1 次的直線.
為什麼呢?
如果乘法前 input 就已經是 2 條 2 次曲線, 相乘後的曲線會是 4 次曲線.
乘法的過程中, 我們會讓 A B C 各自算出 u1 * v1, u2 * v2, u3 * v3 .
過這三點如果只用 2 次曲線, 重建出的 secret 不會是 u * v . 必須用 4 次曲線.
但我們只有 3 個 party, 是無法決定 4 次曲線的.
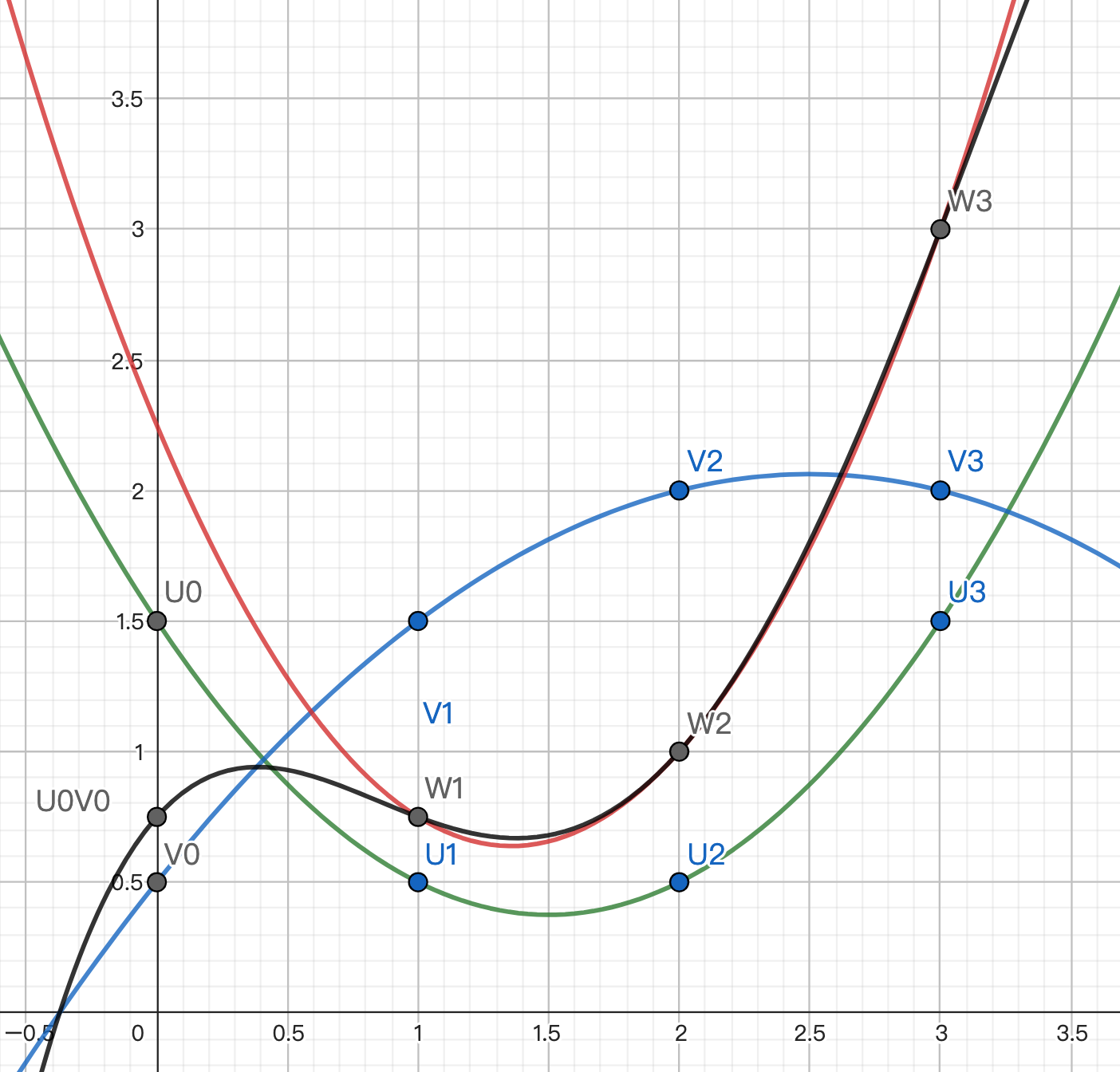
以上圖為例:
綠色 polynomial U 代表的 secret 是 1.5 .
藍色 polynomial V 代表的 secret 是 0.5 .
我們希望找到一條 polynomial 代表 1.5 * 0.5 = 0.75 .
A B C 各自相乘 U V 的 shares 會得到 W1 W2 W3.
如果只用 2 次曲線去 interpolate, 會得出沒有通過 0.75 的, 不正確的紅色曲線.
而黑色的 polynomial U * V 有通過 0.75. 可是 U * V 是 4 次的曲線. 用 3 個 party 的點無法決定.
所以乘法前必須是 2 條 1 次的直線, 相乘出來的 2 次曲線才不會 degree 過高. (degree * 2 + 1 <= 人數)
但如果下一個 gate 又是 “*” gate 呢? 不就又 2 + 2 = 4 了嗎?
因此我們需要對 U * V 做 "degree reduction".
也就是先從 2 條 1 次直線算出 U * V 和其 y 軸交點, 再用一條通過這個交點的 1 次直線來取代它.
這樣我們的 output 就能仍然維持在 1 次直線. 做更多乘法也沒有問題.
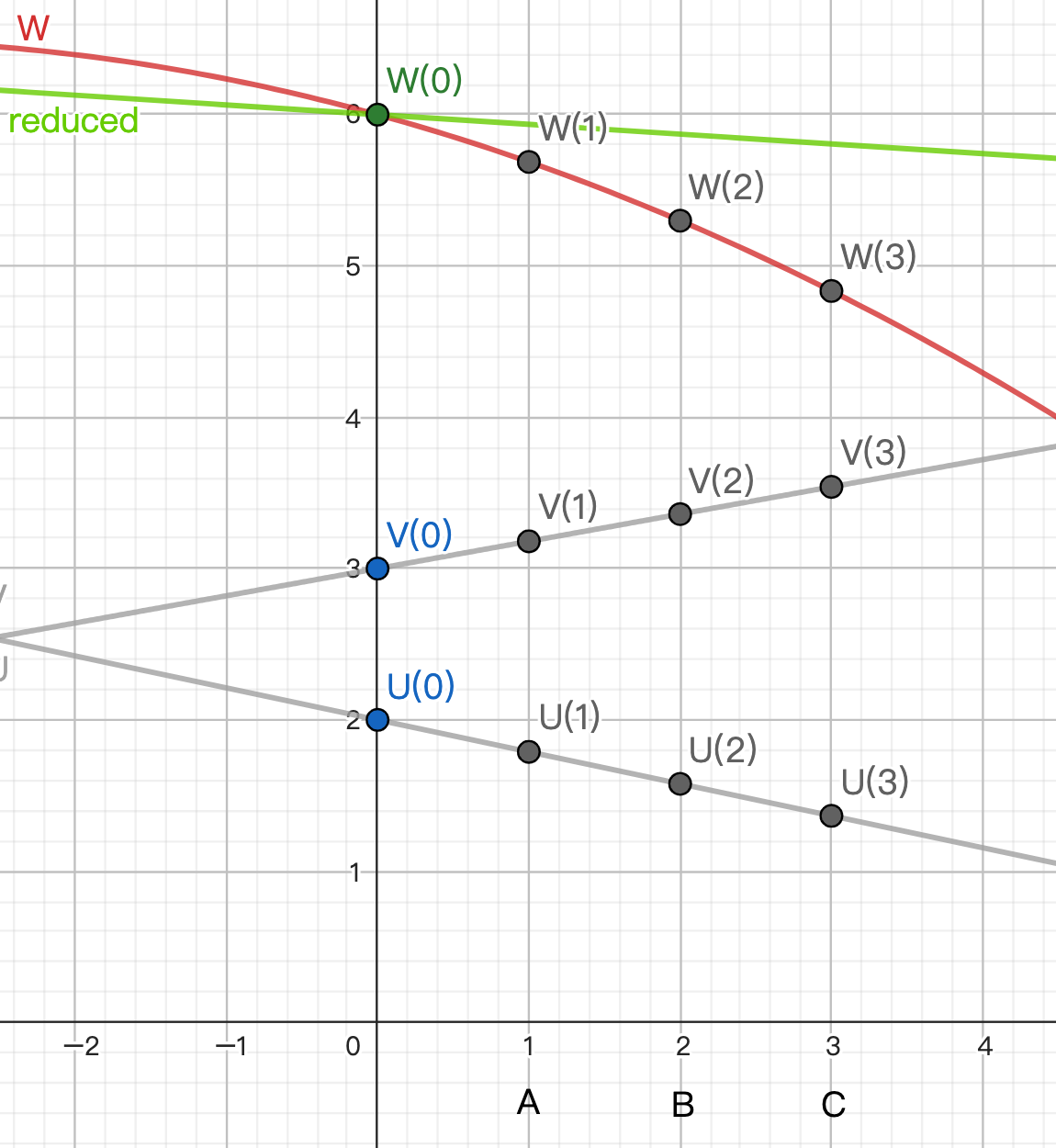
Degree Reduction
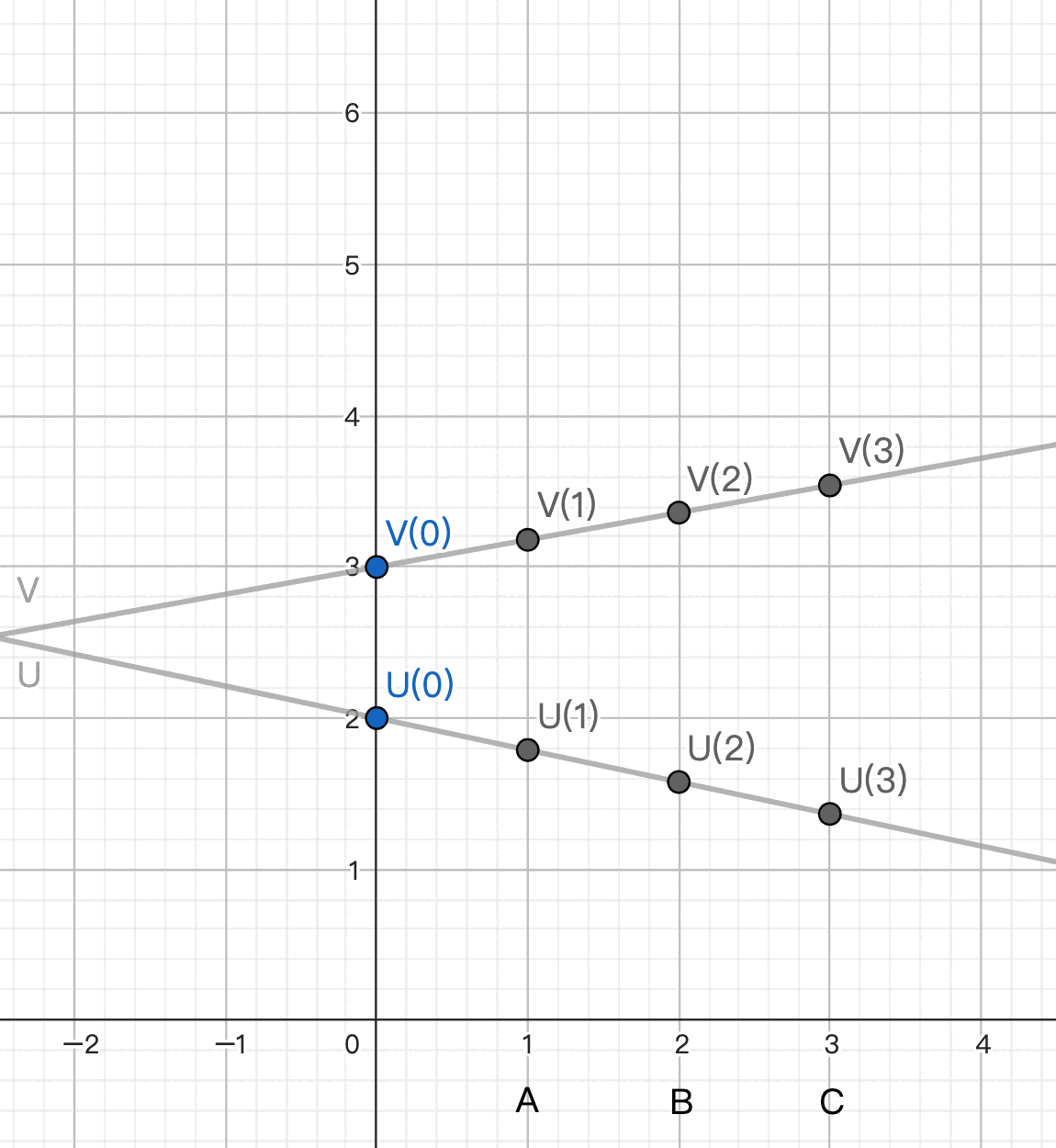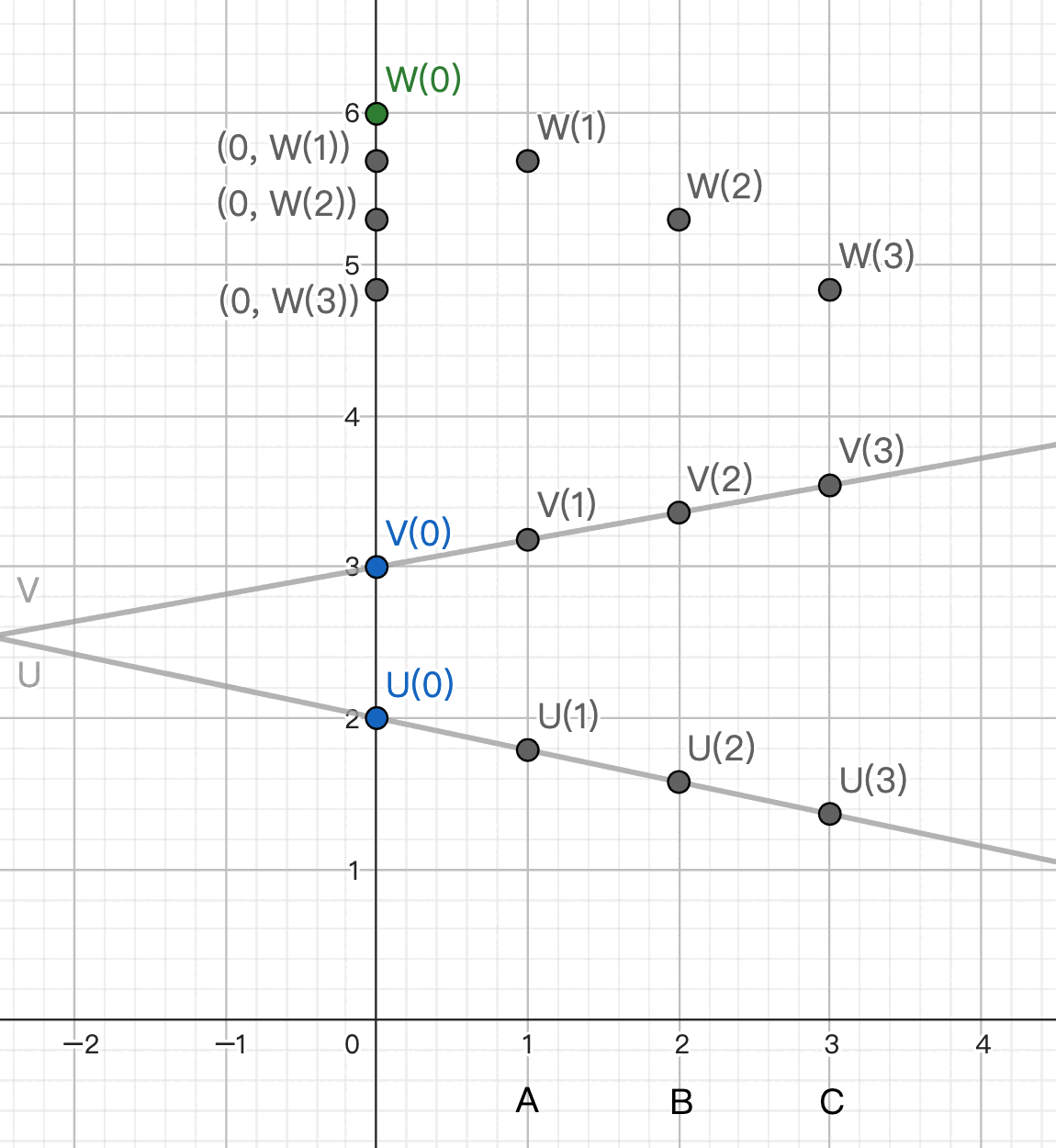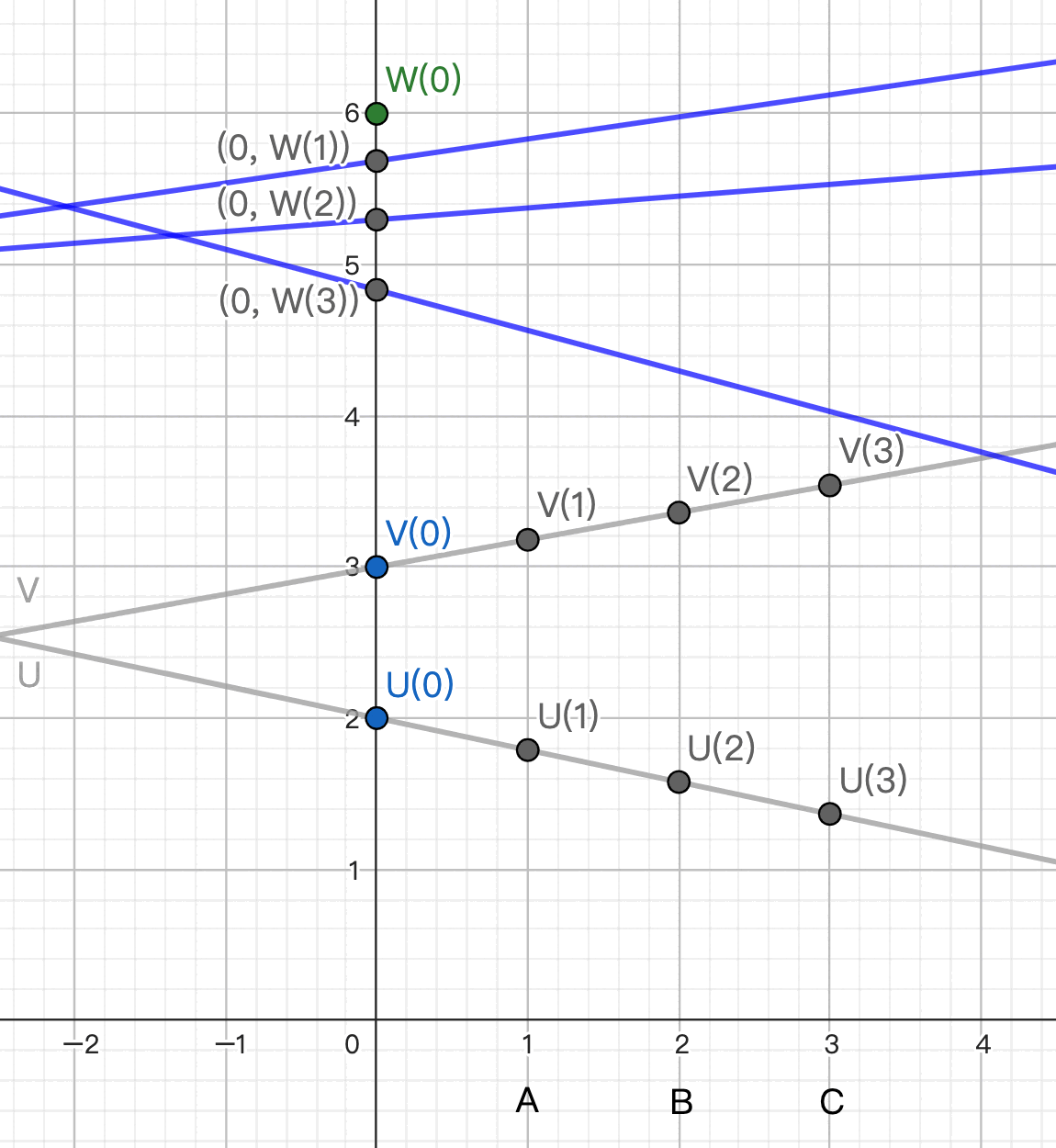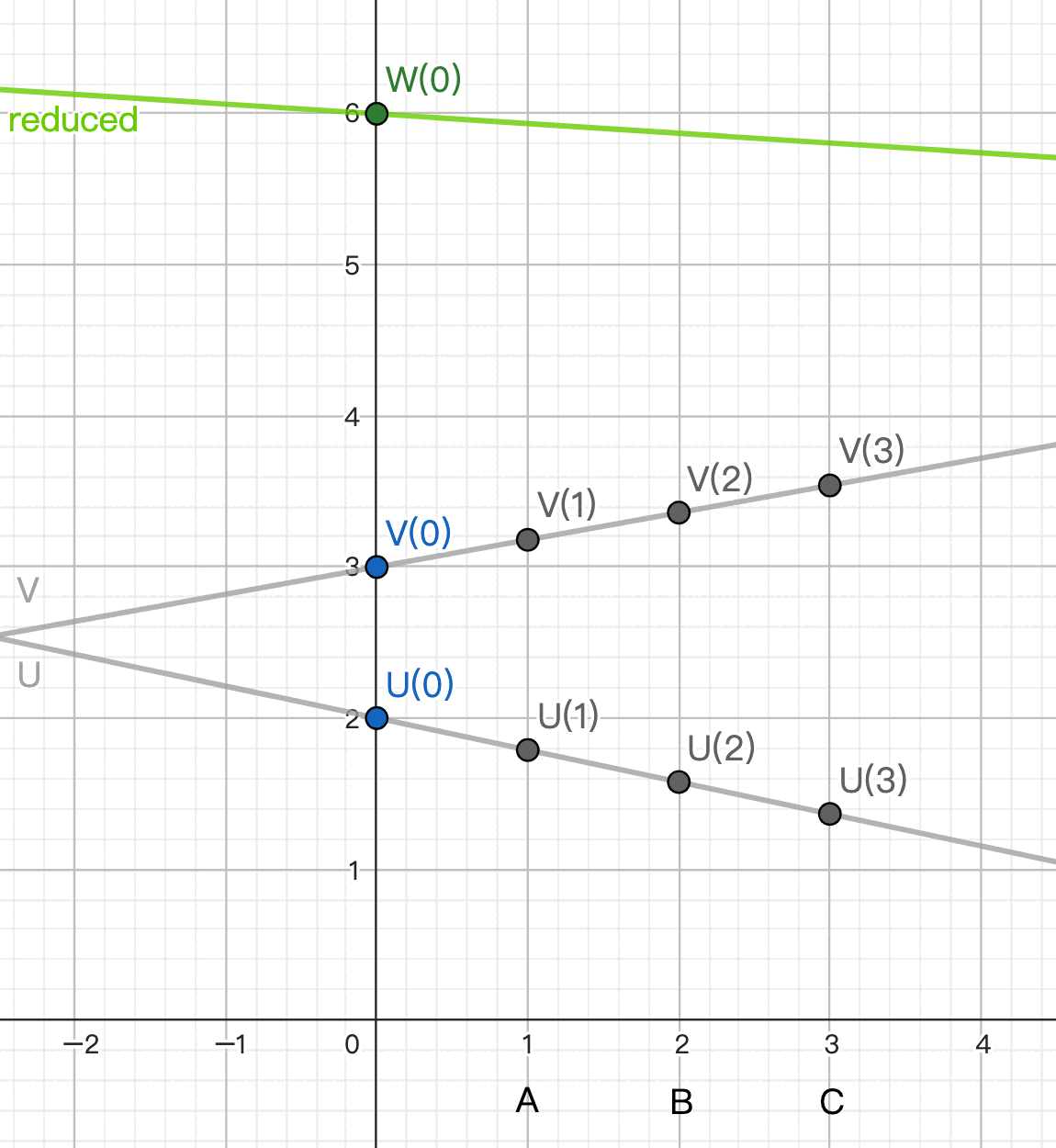
假設 polynomials U, V 為兩直線. Let W = U * V 為二次曲線.
我們想找一條過 (0, W(0)) 的一次直線取代 W, 用這條直線的 shares 作為結果.
步驟如下:
A 獨自算出 W(1) = U(1) * V(1)
B 獨自算出 W(2) = U(2) * V(2)
C 獨自算出 W(3) = U(3) * V(3)
由於 Shamir’s secret sharing 的特性, W(0) 可以簡單表達成 W(1) W(2) W(3) 的 weighted sum, 其 weight 為 (3, -3, 1).
也就是 W(0) = 3 W(1) + (-3) W(2) + 1 W(3) [link]
我們想辦法把上面式子中的 W(1) W(2) W(3) 換成低次的 shares, 則可得到一組 W(0) 的低次的 shares. 作法如下:
A 選一條 random 的 1 次直線經過 (0, W(1)), 把 W1 分成 shares 分給 B C.
B 選一條 random 的 1 次直線經過 (0, W(2)), 把 W2 分成 shares 分給 C A.
C 選一條 random 的 1 次直線經過 (0, W(3)), 把 W3 分成 shares 分給 A B.
現在 A B C 共同持有 [W(1)] [W(2)] [W(3)], 也都知道 weight (3, -3, 1),
所以可以各自計算 weighted sum, 讓三人手上有一組新的 shares 3 [W(1)] + (-3) [W(2)] + 1 [W(3)]. [link]
而這組 shares 代表的 secret 就是 W(0) = U(0) * V(0) = u * v.
穿過這組 shares 的多項式的 degree 和 input 一樣, 只需要 1 次直線. [link]
總結
在 BGW 中, 我們用 Shamir’s secret sharing 來拆分/合併 shares.
加法不需要溝通, 可以各自計算.
乘法在各自乘完後, 還要互相溝通才能降低 degree. 作法是把交點用 weighted sum 表示, 再用低次多項式的 shares 來組成交點的 shares.
這篇用 3 個 party 為例, 過程中所有多項式的 degree 都不能超過 2. 更多 party 的 case 還請自行 generalize.