BMR
在前面的 GMW 和 BGW 中, 我們看到這些 protocol 可以處理兩人以上的計算.
但是因為 “∧” gate 和 “*” gate 的關係, party 間需要跑很多 rounds. (隨 circuit depth 而變)
BMR 想: 我們能否處理兩人以上的計算, 但是卻像 Yao’s Garbled Circuit 一樣, 只要跑 constant rounds 就好了呢?
一起 garble
在 Yao’s GC 中, 一個人產生 garbled table, 一個人 evaluate.
而在 BMR 中, table 是所有人用比較簡單的 MPC protocol 一起生的, 有通訊.
而單一 party 拿到所有 input 後就可以自行 evaluate 整個 circuit, 不用 gate by gate 的通訊.
由於生 table 的時候是平行對所有 gate / wire 一起生的, 所以所需的 rounds 和 depth 無關.
在 Yao’s GC 中, output lable 是用兩個 input labels encrypt 起來的. 確保 evaluate 時只能開的了其中一個.
BMR 中也是這樣. 而這兩個 labels 現在變成每個 party 各拿一部分, 像這樣:
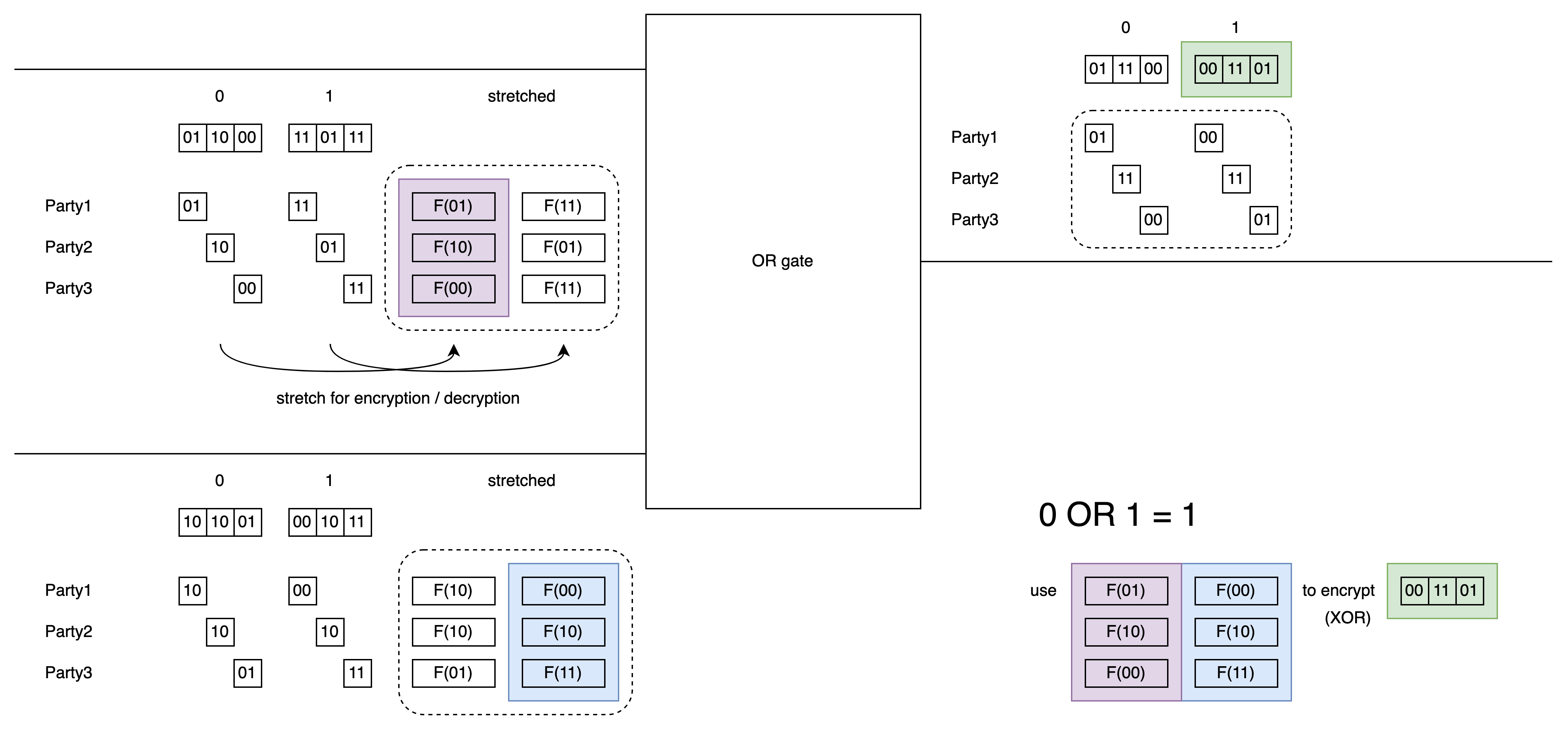
這邊以 OR gate 為例, 計算 4 個 ciphertext 中的其中 1 個 row: 0 OR 1 = 1 .
每個 party 用 PRF 或 hash function 把自己手上的一部分 label 拉長(stretch), 把對應的 output label encrypt (XOR) 起來.
這個 ciphertext 是用 custom 的 MPC protocol 計算出來的. 就是把 7 個 (或 3 個) bit string XOR 在一起而已.
(比方說可以用 先前提過的 protocol)
而圖中虛線框起來的部分是 MPC 的 input. 因為 PRF / hash 已經 local 算過了, 所以 MPC 是簡單的.
我希望看了圖之後, 書中的式子 (3.1) 應該變得比較容易.
\[e_{v_a,v_b} = w_c^{v_c} \bigoplus_{j=1..n} (F(i,w_{a,j}^{v_a}) \oplus F(i,w_{b,j}^{v_b}))\]Evaluate
Evaluate 的人到時候拿到兩個 labels 先切斷, 拉長, 再 decrypt 出 output label.
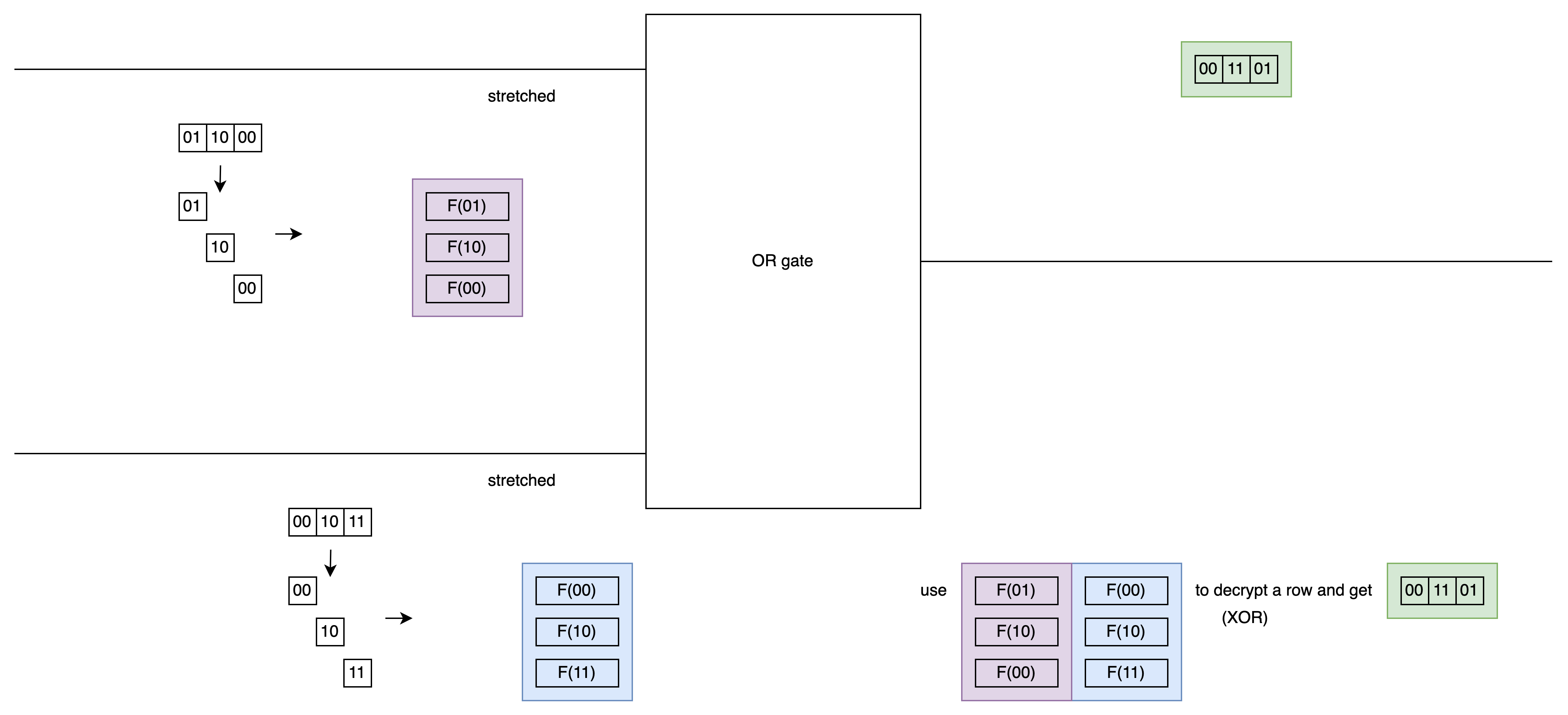
不過觀察上圖: 如果是 Party1 在 evaluate, 當他看到 “011000” 最前面的 “01” 時, 會發現和自己這個 wire 的 label 0 一樣. 這樣就會洩密了.
所以 BMR 還加上了一個 flip bit 的設計. 雖然 Party1 還是可以比對 label, 但是如果不知道這個 wire 的 flip bit, 就不知道 label 真正代表的值是什麼.
Flip bits
對每一個 wire, 每個 party 都 random 一個 flip bit.
這些 flip bits 通通 XOR 起來的值, 就作為這個 wire 的 flip bit.
每個 party 只知道自己的 flip bit.
沒有人知道 intermedia wires 的 flip bit.
如果 flip bit 是 0 就沒有影響.
如果 flip bit 是 1, 則運算中本來要拿 label 0 的就會去拿 label 1, 要拿 label 1 的就會去拿 label 0.
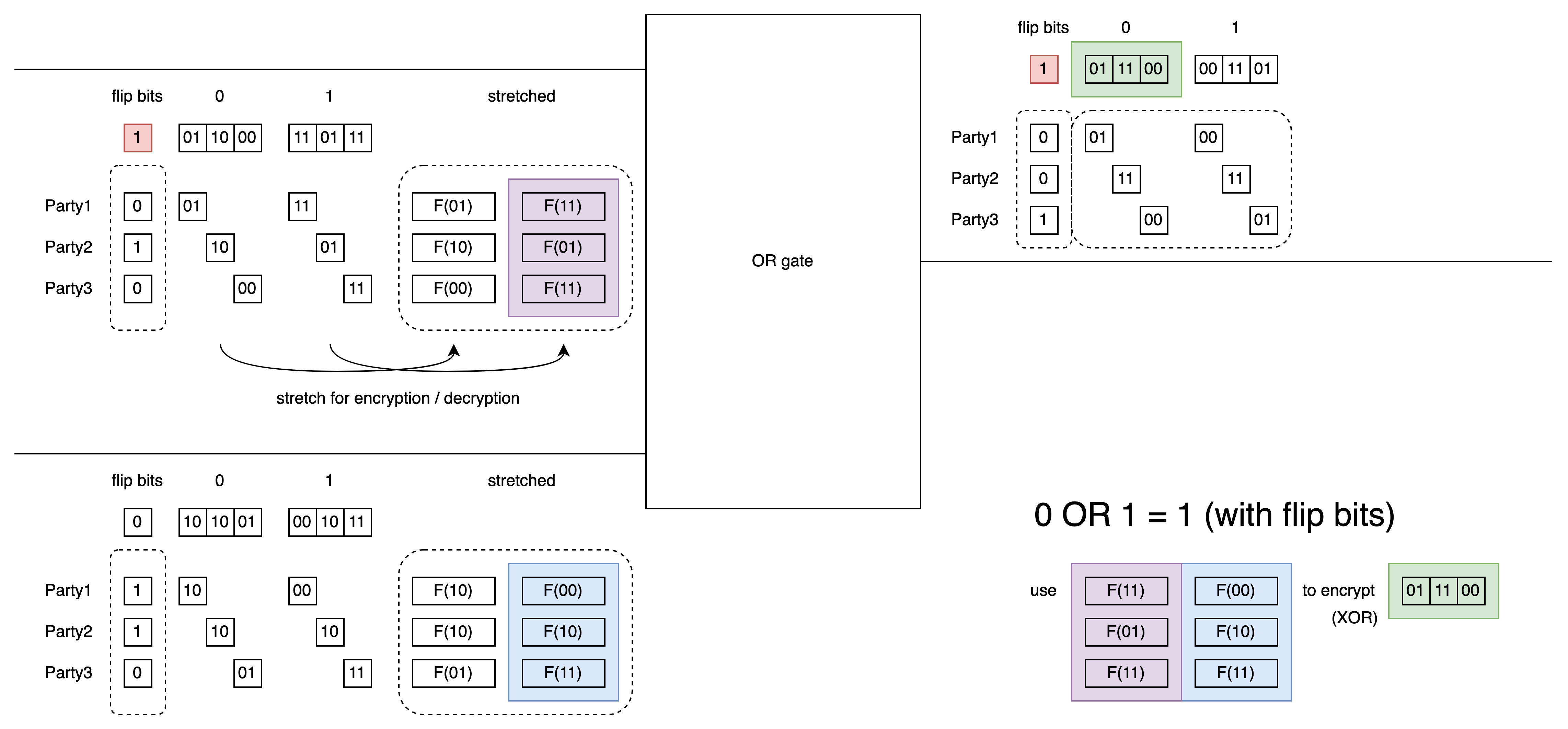
上圖同樣是計算 0 OR 1 = 1 的 ciphertext.
注意第一個 input label 和 output label 這兩個 wire 的 flip bits 為 1.
所以這兩個 wire 選取的 label 就反過來了.
這個邏輯是在書中的 Figure 3.3 .
\[e_{v_a,v_b} = w_c^{v_c \color{blue}{\oplus f_c}} \bigoplus_{j=1..n} (F(i,w_{a,j}^{v_a \color{blue}{\oplus f_a}}) \oplus F(i,w_{b,j}^{v_b \color{blue}{\oplus f_b}}))\]注意 w 右上角的 index 現在都多了 flip bit f 的影響.
最後 parties 也把 input wire 實際的 bits 交給這個比較簡單的 MPC, 算出 input wires 的 label. 公開後就可以 evaluate.
總結
在 BMR 中, 我們用比較簡單的 MPC protocol 來實作真正想要的 function 的 MPC.
BMR 擴充了 Garbled Circuit, 得到了多於兩人的, constant round 的 MPC protocol.
TODO: 書中對底層簡單 MPC 的實作比較沒有描述, 還要看其他參考資料.