Function Secret Sharing / Distributed Point Function
Function Secret Sharing (FSS) 想做到的是: 把一個 function f split 成 N 個 function 給 N 個 party.
對於同一個 input x, party 0 計算 f0(x), party 1 計算 f1(x), …
這些 value 會是原本 f(x) 的 additive shares, 也就是 f0(x) + f1(x) + … = f(x).
不同的 function family 可能有不同的 FSS 的作法. 以下介紹 Boyle et al. 針對 Distributed Point Function 的作法. (定義和應用請參考前一篇文章)
Boyle’s Construction
這邊我們看一個特例: f 的 domain 為 [0, 7], 只有在 x = 5 時 f(x) = 1. 只有 P0 P1 兩個 party.
Boyle 的方法是計算一棵想像的 tree. 由 P0 P1 分別計算其 shares.

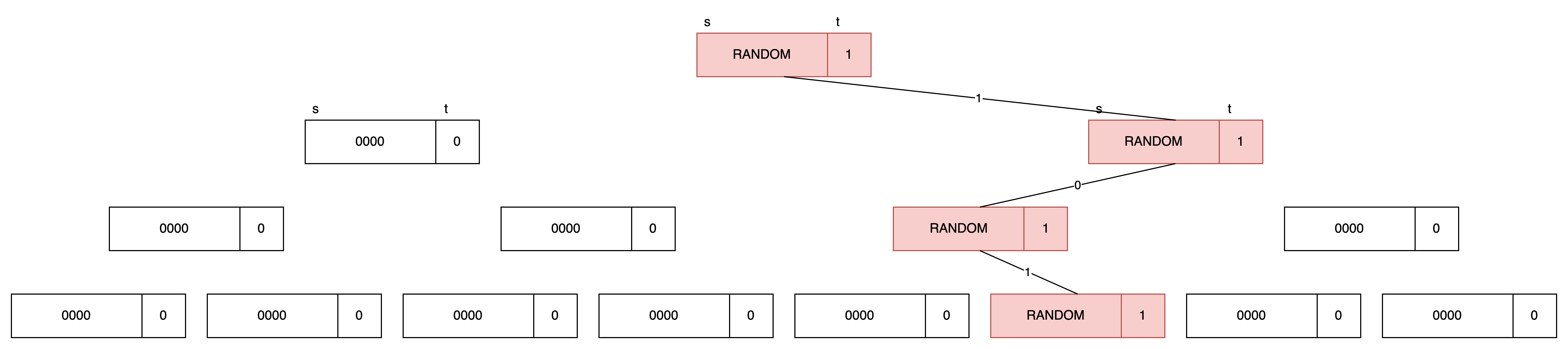
我們希望只有 f(5) 這個 leaf 為 1.
計算 f(5) 的這條 “1-0-1” 的 path 叫做 “special evaulation path”. 從 root 往 leaf 計算.
每個 node (s, t) 是由 lambda-bits 的 seed s 和 1-bit 的 control bit t 所組成的.
重要的 invariants: 我們希望計算過程中, 如果偏離了 special evaluation path 的話, 這個 node 就會是 (00….0, 0).
(OFF, 黑色. P0 P1 持有完全相同的 bits.)
如果沒有偏離, 則這個 node 會是 (random bits, 1).
(ON, 紅色. P0 P1 持有不完相同的 bits.)
最後我們輸出 leaf 的 control bit. 只有 leaf 5 的 control bit 會是 1.
注意整個過程中不能讓 P0 P1 發現 f(5) = 1.
Generation / Evaluation
Boyle’s construction 有兩個 algorithm.
Gen() 可以把 f 拆成 f0 和 f1, 分別用 key0 key1 來描述. 分給 P0 P1.
P0 把 x 和 key0 交給 Eval() 就能算出 f0(x).
P1 把 x 和 key1 交給 Eval() 就能算出 f1(x).
我們從 evaluation 的角度來反推一開始的 generation 要準備怎樣的 key.
Evalutation 的方式和 GGM 的 “PRNG -> PRF” 作法類似: 從 root 的 seed 開始, 每次用 PRNG 把 node 拉長成兩倍, 切開變成兩個 child node. (另外延伸兩個 control bits 的長度)
一開始 Gen() 生出兩個 uniformly random 的 bit string 給 P0 P1 當成 root 的 seeds.
讓 P0 P1 各自用 PRNG 往下生出 2 4 8 … 個 child node.
但是很顯然這樣做出來的 nodes reconstruct 起來不會滿足前面的 invariants.
所以 Gen() 另外在 tree 的每個 level 準備了 “correction words” (CW), 可以把 PRNG 生出來的 bits 再修成符合 invariants 的樣子. 在 reconstruct 出來的 tree 中, 這個修改會把偏離 special evaluation path 的 child node 消成 0, 而另一個 child node 仍然是 random bits.
Conditional Correction
實際在 Eval() 中, 兩個 party 各自進行 “conditional correction”: 如果手中的 control bit t = 1, 就 XOR correction word 來修正, 否則不修正.
如果 P0 P1 手中拿的是 control bit t = 0 的 shares, 則可能是 (0, 0) 或 (1, 1).
因為 P0 P1 修正兩次等於沒有修正, 所以不論是 (0, 0) (1, 1) 都不會改變 reconstruct 出來的結果.
s0 ⊕ s1 = (s0 ⊕ CW) ⊕ (s1 ⊕ CW)
如果 P0 P1 手中拿的是 control bit t = 1 的 shares, 則可能是 (1, 0) 或 (0, 1).
剛好會讓 reconstruct 出來的結果被 CW 修正一次.
(s0 ⊕ CW) ⊕ s1 = s0 ⊕ (s1 ⊕ CW) = (s0 ⊕ s1) ⊕ CW
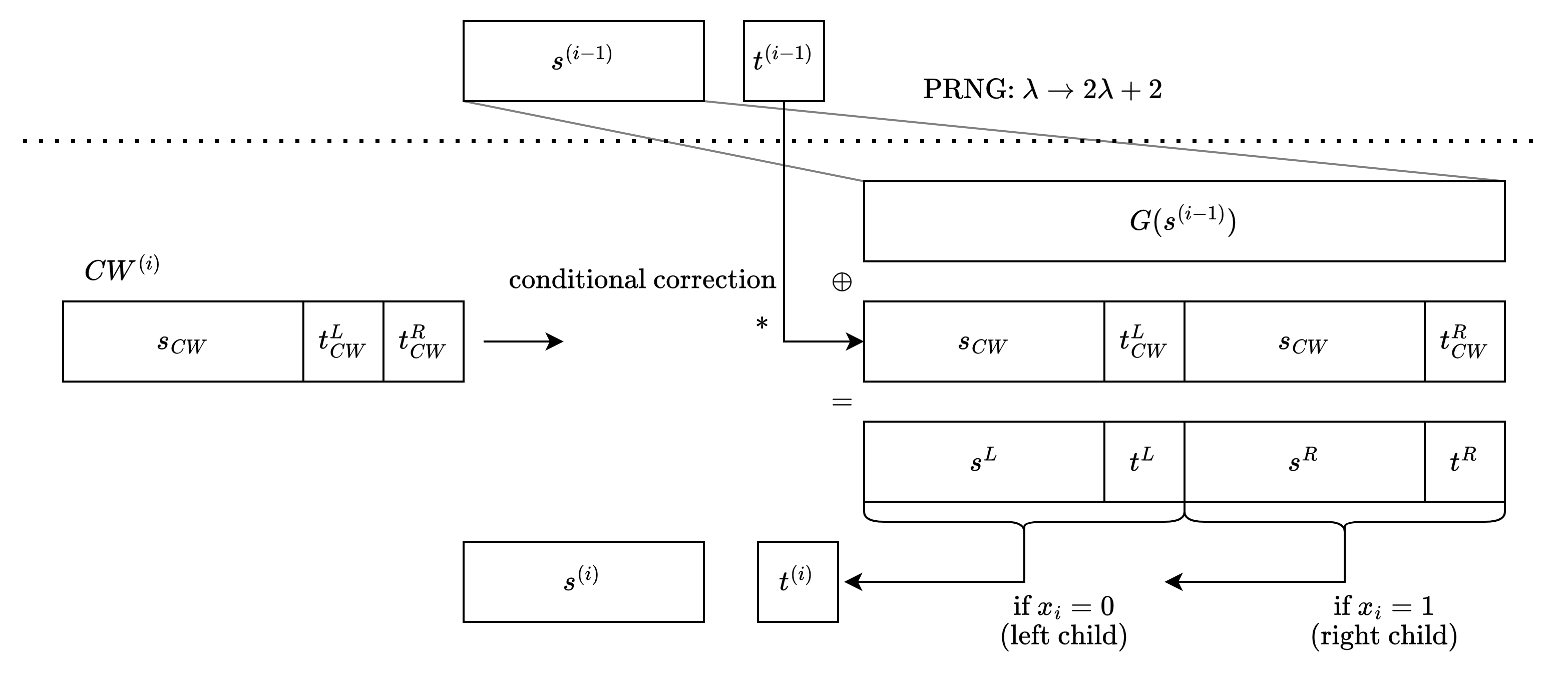
Levels and Invariants
我們從最上面的 level 開始看. 因為 root 一定在 special evaluation path 上, 我們讓其 control bit t = 1.
接下來往下產生每個 level.
如果 parent node 在 special evaluation path 上, 則用 CW 把偏離的 child node 修改成 s = 0, t = 0. 也用 CW 確保沒偏離的另一個 child 是 s = random, t = 1.
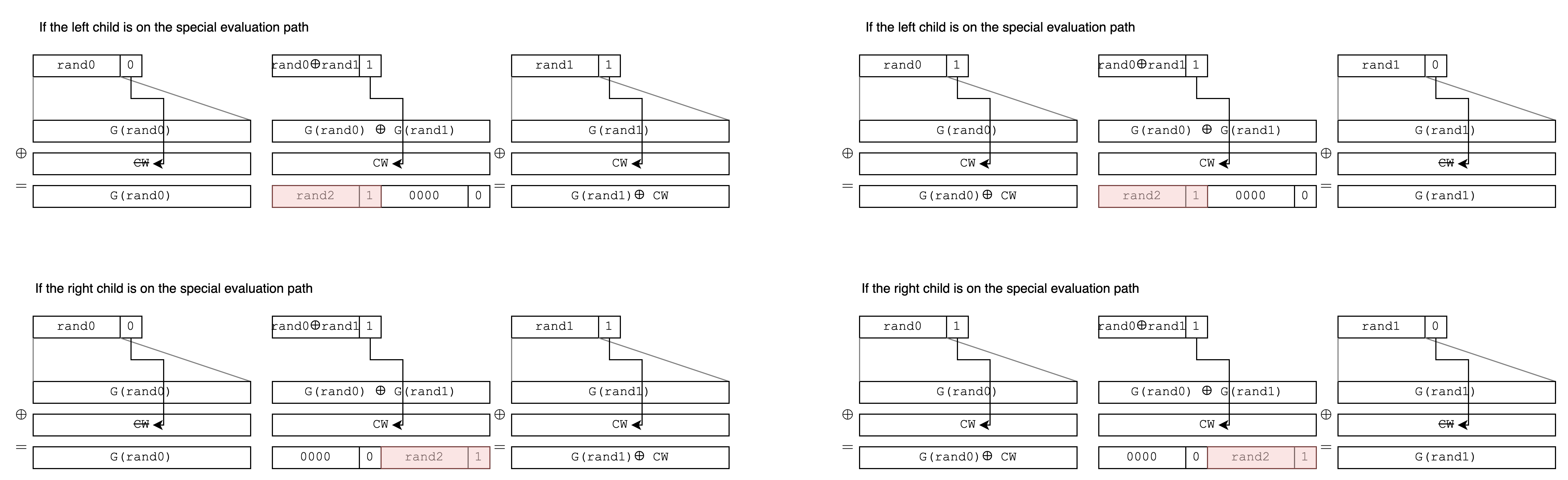
如果 parent node 已經不在 special evaluation path 上, 則會是 s = 0, t = 0 的樣子. 因為 t = 0, 所以 conditional correction 不起作用(也不需要起作用). 兩個 child node 仍然會是 s = 0, t = 0.

由於 CW 不需要修正已經偏離的 node, 而每個 level 又只有一個還在 special evaluation path 的 node, 所以每個 level 只需要準備一個 CW 就好了.
Optimization: 因為我們只需要確保把一個 child 修正成 0, 另一個 child 的 s 可以是任意的 random string, 所以可以複製半邊的 CW, 節省一半的空間.
Keys

在 Gen() 的過程中, 一開始先為 P0 P1 各自 random 出 root 的 seeds.
root 必定在 special evaluation path 上, P0 P1 的 control bits 直接指定為 (0, 1), 不用儲存在 key 裡.
假設我們有以下的 4 -> (4 + 1 + 4 + 1) bits 的 PRNG G():
0000 0001000101
0001 0100100010
0010 1111010111
0011 1010100011
0100 0101010101
0101 0000011001
0110 1001000111
0111 1010011110
1000 0100110000
1001 1010101010
1010 1110110000
1011 1101100011
1100 1111000000
1101 0111101101
1110 1001100001
1111 1001110011
假設 random 給 P0 P1 seed 分別 “0100” 和 “1110”.
透過 G 展開後會是 “0101010101” 和 “1001100001”.
為了保持 invariants, 我們可以逐步推導出每個 level 在 special evaluation path “1-0-1” 所需要的 CW.
後記
Boyle 在 BIU 講課的內容很值得看: FSS Part 2 - Elette Boyle.