GMW / GMW87
前面介紹了 1986 年的 Yao’s Garbled Circuit, 是適合兩個 party 的 protocol.
1987 年 Goldreich-Micali-Wigderson 提出的 protocol 則可以用於更多 party 的場景.
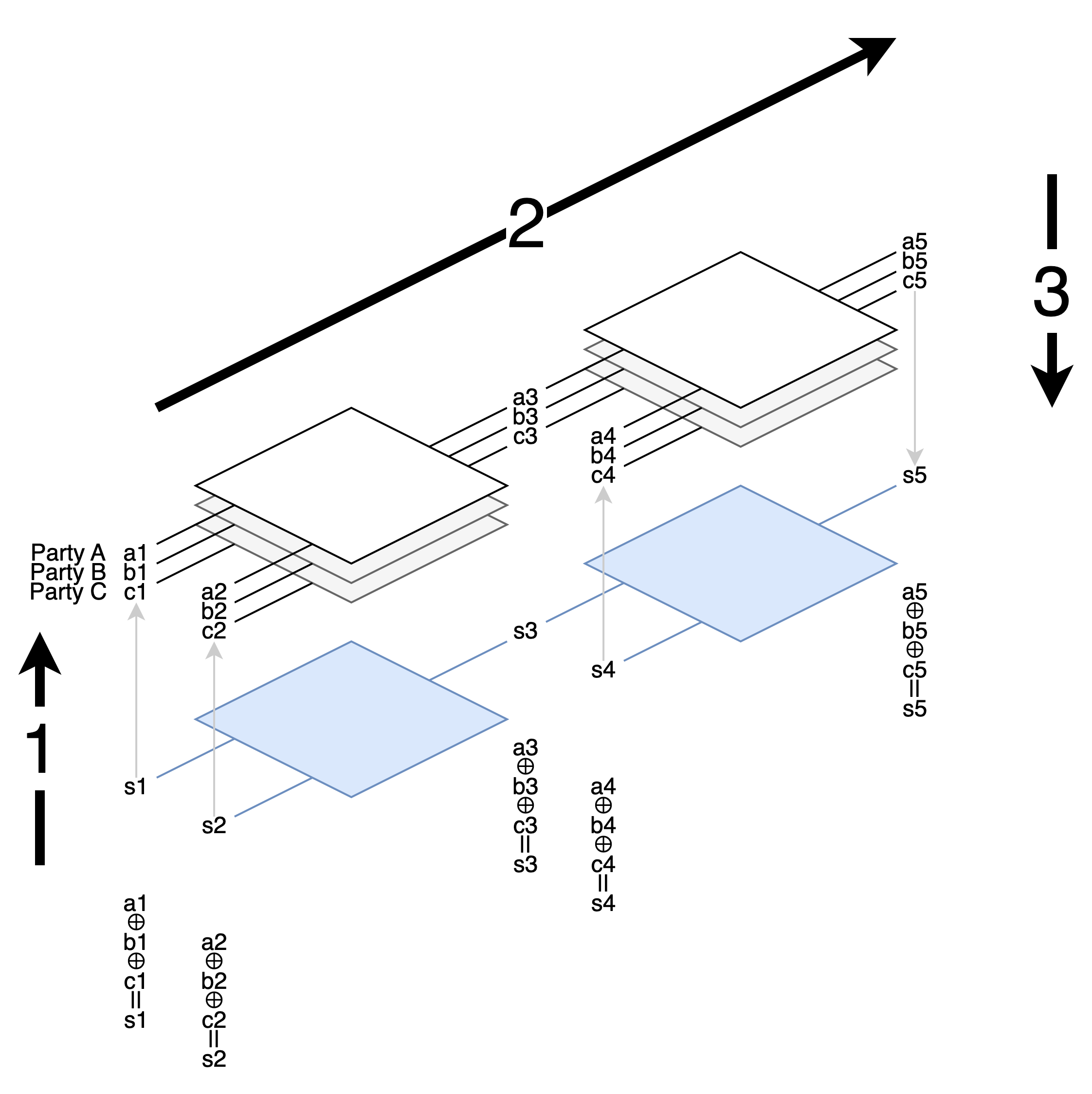
每個 party 現在有自己的一份 circuit 和 shares of wire values.
執行上分成三步驟
- 每個持有 input wire value 的 party, 把 value 拆成 shares 分給每個 party.
- 依照 topological order, 用每個 gate 的規則計算 output wire 上的新的 shares.
- 把最後的 output wires 的 shares 合併, 再公布答案.
我們用 [value] 來代表 value 拆開的 shares. 舉例來說, 像原本 (a ⊕ b) ∧ c 的計算, 會變成
- 拆開 a b c 成 [a] [b] [c], 分給其他人.
- 想辦法從 [a] [b] 算出 [a⊕b], 以及從 [a⊕b] [c] 算出 [(a⊕b)∧c]
- 從 [(a⊕b)∧c] reconstruct 出 (a⊕b)∧c
而整個 protocol 的每個步驟都滿足 “input 拆開 / 計算 / output 合起來 = 直接計算” 的性質. 所以逐步算完的答案會是對的.
我們來看 GMW 實際上是怎麼實作的.
input 拆開 / output 合起來
如果 A 持有 input s1, 要分開讓 A B C 三個人持有 shares.
GMW 這邊用 XOR 的 additive shares, 也就是拆開成 s1 = a1 ⊕ b1 ⊕ c1 .
A 可以在其中兩份取亂數, 再從 s1 扣掉這兩份就能得到第三份 share 了.
舉例來說, 如果 s1 是 1, A 取亂數得 a1 = 0, b1 = 1, 則算出 c1 = 0.
A 留著 a1, 把 b1 c1 分給 B 和 C.
合併也只要通通 ⊕ 起來就好了.
計算 circuit
這裡用的是由 NOT / XOR / AND gates 組成的 boolean circuit.
用這組 gates 的好處是: NOT / XOR 可以每個 party 分開算, 不用互相溝通. 只有 AND 需要 party 間的溝通.
每個 gate 的規則如下:
NOT gate
第一個 party 把自己的 input share reverse 就好. 其他 party copy input 成 output. 這樣就能得到一組新的 shares.
(!a1) ⊕ b1 ⊕ c1 = !(a1 ⊕ b1 ⊕ c1)
另外在這個例子裡可以看到, 我們注重的是所有 shares 合起來的 output 是否滿足這個 gate 的邏輯. 單一 party 的 output 不用滿足這個 gate 的邏輯.
XOR gate
每個 party 都分別照一般的 XOR 規則個別計算, 就能得到一組新的正確的 shares.
已知
s1 = a1 ⊕ b1 ⊕ c1
s2 = a2 ⊕ b2 ⊕ c2
如果令新的 shares a3 b3 c3 是每個 party 分別計算 ⊕ 的結果:
a3 = a1 ⊕ a2
b3 = b1 ⊕ b2
c3 = c1 ⊕ c2
那會有 a3 ⊕ b3 ⊕ c3 = s1 ⊕ s2 嗎?
有的!
a3 ⊕ b3 ⊕ c3
= (a1 ⊕ a2) ⊕ (b1 ⊕ b2) ⊕ (c1 ⊕ c2)
= (a1 ⊕ b1 ⊕ c1) ⊕ (a2 ⊕ b2 ⊕ c2)
= s1 ⊕ s2
AND gate
複雜的在這裡. 每個 party 獨自計算 AND 的話, 合起來會不對. 所以要互相溝通.
AND gate: 2 parties
先講只有 2 個 party A B 的情形.
a1 a2 a3
⊕ ⊕ ⊕
b1 b2 b3
= = =
s1 ∧ s2 = s3
A B 手上各有 shares a1 a2 b1 b2. 現在想求出一份 a3 b3 滿足上面的性質.
A 對 B 說: "我知道 a1 a2, 但我不知道你的 b1 b2. 所以我對每一組可能的 b1 b2 算出了對應的 s3. 我先從 s3 裡面拿走我的 share a3, 剩下的 b3 你再用 Oblivious Transfer 來拿走吧."
這邊我以 a1 = 0 a2 = 1 為例. 假設 A 取亂數決定了 a3 = 1. 求所有可能的 b3.
a1 a2 b1 b2 s1=a1⊕b1 s2=a2⊕b2 s3=s1⊕s2 a3 b3=s3⊕a3
0 1 0 0 0 1 1 1 0
0 1 0 1 0 0 0 1 1
0 1 1 0 1 1 0 1 1 <==
0 1 1 1 1 0 1 1 0
假設 B 手上是 b1 = 1, b2 = 0.
B 和 A 進行 1-out-of-4 Oblivous Transfer, 拿到對應的 b3 = 1 .
至此, 新的 a3 ⊕ b3 = s3 是一組新的, 滿足上述性質的 shares.
AND gate: N parties
我們看 N = 3 的 case. (其他 case 請自己 generalize)
a1 a2 a3
⊕ ⊕ ⊕
b1 b2 b3
⊕ ⊕ ⊕
c1 c2 c3
= = =
s1 ∧ s2 = s3
已知 a1 b1 c1 和 a2 b2 c2 這兩份 shares. 想要求一份新的 shares a3 b3 c3 滿足上面的性質.
套用分配率 (∧ 是 *, ⊕ 是 +)
s3 = s1 ∧ s2
= (a1⊕b1⊕c1) ∧ (a2⊕b2⊕c2)
= ⊕ ( a1∧a2 a1∧b2 a1∧c2
b1∧a2 b1∧b2 b1∧c2
c1∧a2 c1∧b2 c1∧c2 )
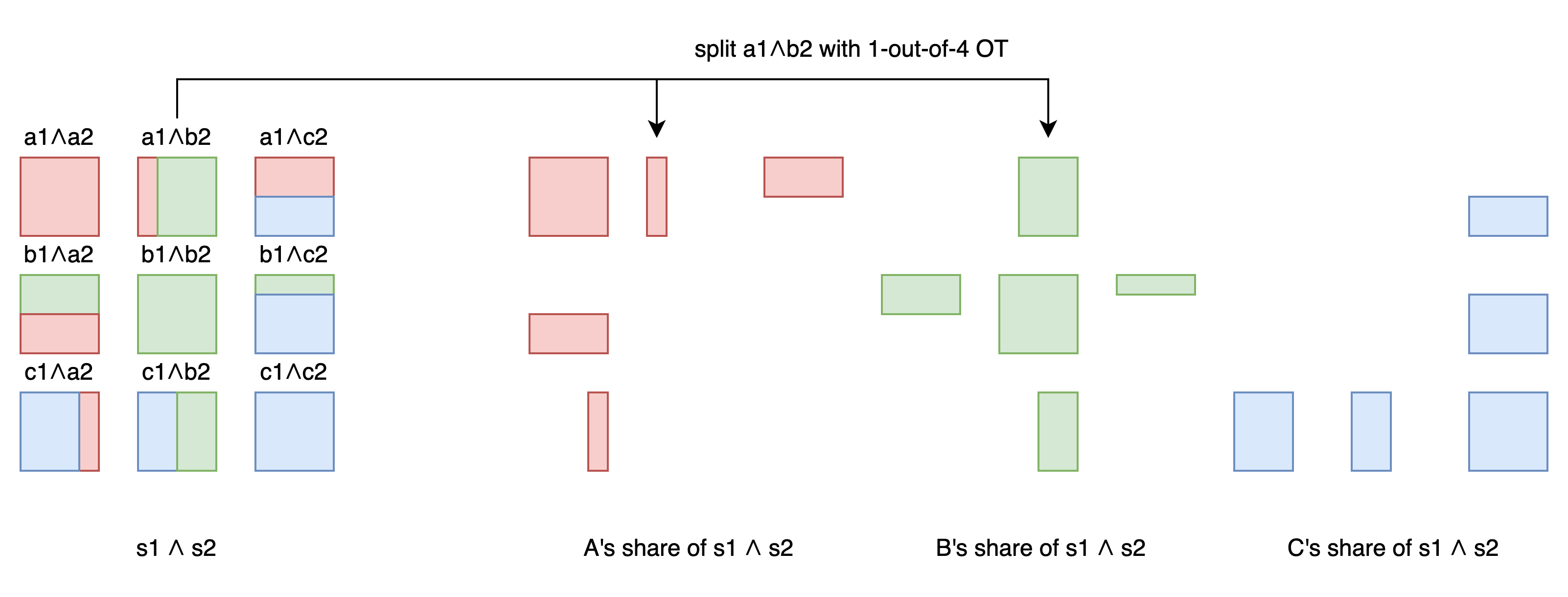
除了對角線的 a1∧a2 可以 A 自己算, b1∧b2 可以 B 自己算, c1∧c2 可以 C 自己算之外, 其他都需要溝通.
像 a1∧b2 就需要 A B 手上的資訊. 所以 A B 進行前面說過的 1-out-of-4 OT, 兩人各自得到 a1∧b2 拆出來的兩個數字, 這兩個數字合起來可以得到 a1∧b2 .
用同樣的手法處理 6 個不在對角線上的數字. 每個數字在 OT 後都分成 2 shares.
最後每個人手上都有一個獨自計算的對角線的 share, 和四個和別人 OT 得到的 shares. 5 個 shares XOR 起來會是屬於自己的 s3 的 share.
尾聲
在 GMW 中, 我們把 function 用 boolean circuit 來表達, 並用 additive share 的方式來拆分和合併. 步驟中用 OT 來互相溝通.
在下一篇的 BGW 中, 我們將把 function 用 arithmetic circuit 來表達, 用多項式來拆分 shares. 而且不用 OT.