Garbled Circuit - FreeXOR
執行 Garbled Circuit protocol 的 bottleneck 在於傳輸大量 gate 的 ciphertexts.
FreeXOR 和本書 Section 3.6 的 GESS 一樣, 都是讓 garbled circuit 從 “查表” 回到 “計算”.
也就是說, 如果一個 XOR gate 的 output label 可以由 evaluator 拿著兩個 input labels 跑一段程式就直接算出來的話, 那這個 gate 就不用傳 ciphertexts 了. 因為 local 計算比收送資料便宜很多, 所以這個 gate 幾乎可以看成是 free 的.
How
FreeXOR 有一個規則是: 有個 global 的, generator randomly 選定的 Δ . Circuit 中每個 wire 的 key 0 是由其 key 1 ⊕Δ 得來的. 這規則適用於每一個 gate, 不光是 XOR gate.
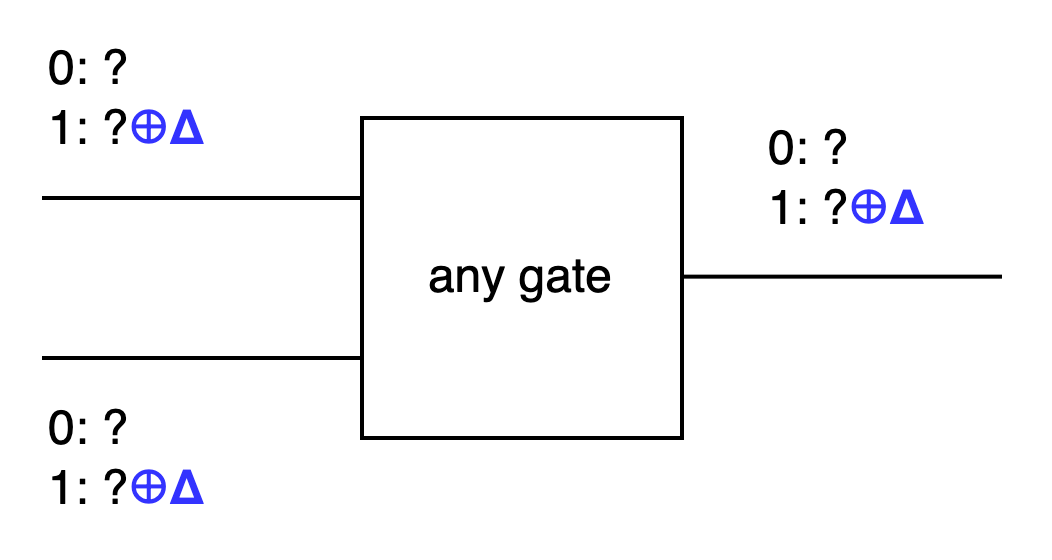
以下用 a b 代表一個 gate 的 input wires, c 代表 output wire. (這裡用比書中簡化的 notation)
如果 wire a 的 key 0 是 a, 那 wire a 的 key 1 就會是 a⊕Δ .
如果 wire b 的 key 0 是 b, 那 wire b 的 key 1 就會是 b⊕Δ .
這裡把整個 circuit 的 gate 分成兩類來處理: XOR 和 non-XOR .
XOR Gates
先看重點 XOR gate.
XOR 原本的 table 是
0 0 0
0 1 1
1 0 1
1 1 0
如果 XOR gate 像前面說的 “要用算的” 的話, 那 output 自然就是 input XOR 起來.
從第一個 row, 0 XOR 0 = 0 來看, wire c 的 key 0 應該是 wire a b 分別的 key 0 XOR 起來, 也就是 a⊕b.
而所有 gate 的 key 1 應該從 key 0 ⊕Δ 得來, 所以 wire c 的 key 1 會是 a⊕b⊕Δ .
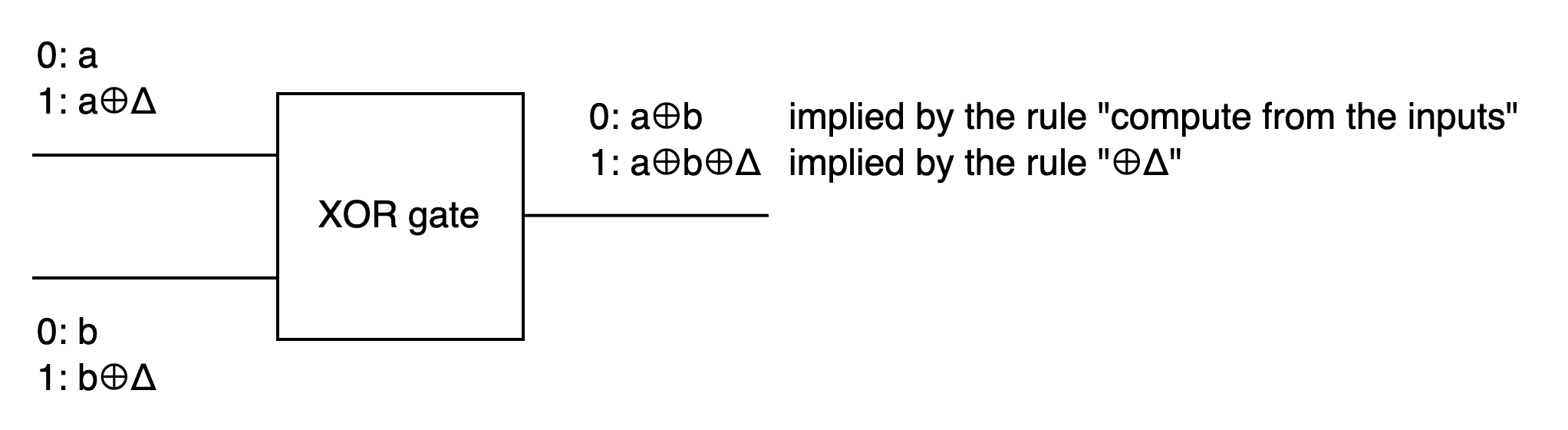
這樣訂出來的 wire c keys (a⊕b, a⊕b⊕Δ), 在另外 3 個 row 也能滿足計算規則嗎?
0 1 1 a ⊕ (b⊕Δ) = a⊕b⊕Δ
1 0 1 (a⊕Δ) ⊕ b = a⊕b⊕Δ
1 1 0 (a⊕Δ) ⊕ (b⊕Δ) = a⊕b ⊕Δ ⊕Δ = a⊕b
剛好可以!
non-XOR Gates
再看 non-XOR gate.
因為這邊我們沒有要用算的, 就還是老實的把 ciphertext 表格建起來. 其中 wire c 的 key 0 就像一般 garbled circuit, 是用 random 出來的, 假設是 c. 而 wire c 的 key 1 必須符合 ⊕Δ 規則, 所以會是 c⊕Δ . 剩下就是依照 gate logic 把 wire c 的 0 1 算出來, 換成 (c, c⊕Δ) 之一, 再 encrypt.
詳細作法
這邊粗略的介紹了 FreeXOR 的概要. Generator 詳細的作法請看書中的 Figure 4.1 . 和前面介紹的 GRR3 一樣, output wire 的 label 和 input 有關, 所以也是要用 topological order.
Evaluator 詳細的作法書中省略了. 想要對答案的話可以看原 paper 的 Algorithm 2.
詳細的 protocol 請看原 paper 的 Protocol 1. (有把 NOT-gate 拿掉)
安全
原 paper 有一段 “Intuition for security”. 大意是: H(a || b || i) ⊕ c 是一種 one-time pad, 而每個 pad value 應該只有用到一次. 當 evaluator 走到一個 gate 時, 兩條 input wire 他應該只知道各一個 label, 所以其他 3 個不該被看到的 output label 是無法被 decrypt 的. 因此 output wire 他也只知道兩個中的一個 label, 對他來說只是個 random string, 推不出原來的 value.
TODO: 詳細的安全證明在原 paper 3.2 “Proof of Security”.
TODO: Choi et al. 提到原 paper 的問題, 指出這邊的 hash 需要 circular correlation robustness 才行.
Combo
FreeXOR 不能搭配 Pinkas 的 GRR2, 但可以搭配 GRR3 .
後來出現的 FlexXOR 可以搭配 GRR2, 不過 XOR 有時會有 cost, 且比較複雜.
再後來的 Half Gates 可以相容 FreeXOR, 且能把 AND gate 壓到只要兩個 ciphertexts, 又相對簡單. 是一個很好的 optimization 組合.
下一篇, 我們來看 Half Gates.
後記
FreeXOR 的第一作者 Vladimir Kolesnikov 是本書的三位作者之一. GESS 也是他的作品.
FlexXOR 本書兩位作者是共同作者.