Garbled Circuit Optimization: Half Gates
The bottleneck in executing the Garbled Circuit protocol is bandwidth.
To reduce the required bandwidth, there are various optimizations aimed at reducing ciphertexts. Compatible optimizations can be combined to achieve even greater power.
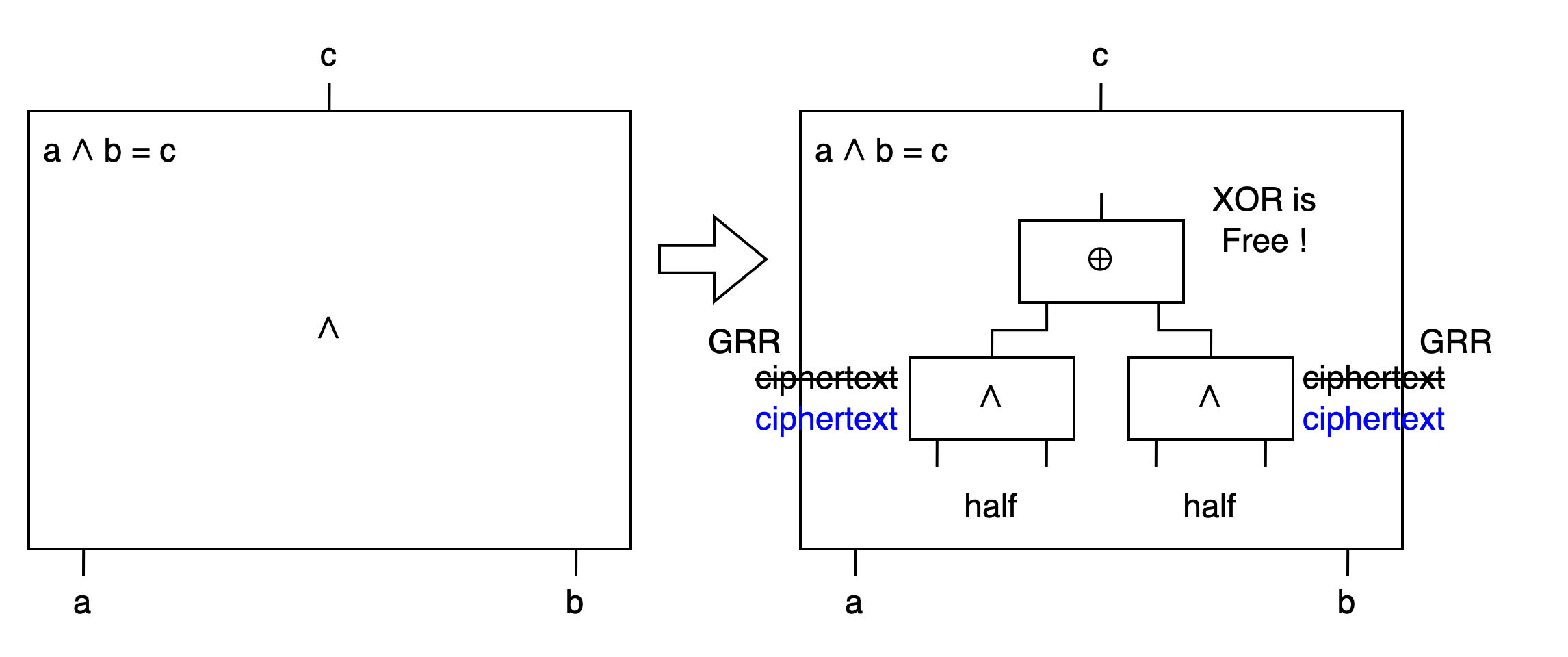
Half Gates is an optimization that can be combined with FreeXOR. While maintaining the advantages of FreeXOR, Half Gates can reduce an AND gate to only 2 ciphertexts! It’s a powerful combination.
Half Gates splits an original AND gate into two half gates, then connects them with XOR. XOR gate can apply FreeXOR, requiring no ciphertext. The two half gates can each apply the GRR3 technique to reduce ciphertexts from two to one. This way, a whole AND gate only needs two ciphertexts, and other XOR gates are still free.
But what is a half gate?
Half Gate
Normally, a gate with two input wires would need 2 * 2 rows to represent 4 possible input combinations.
However, if the value of one of the wires is known, we only need to handle 2 * 1 combinations. We call such a gate a half gate.
But if the gate is deep in the circuit, after complex calculations, why would there still be a wire with a known input???
This was my biggest confusion (and pain) when I first read about this approach.
So, unlike the order in the book and the original paper, I want to first introduce where this known input comes from, then explain how to use this input to reduce ciphertexts.
Where does the known input come from?
In ordinary integers, we have addition and multiplication. For any integers a, b, r, the distributive property holds: a * (b + r) = (a * b) + (a * r).
When we see a regular a * b, if we forcefully apply the distributive property, we can create:
a * b
= a * (b + r - r)
= a * (r + (b - r))
= (a * r) + (a * (b - r))
From the outside, it would be using a + to connect two *.
In boolean logic, ∧ is *, ⊕ is + (and also -).
So we have the distributive property a ∧ (b ⊕ r) = (a ∧ b) ⊕ (a ∧ r).
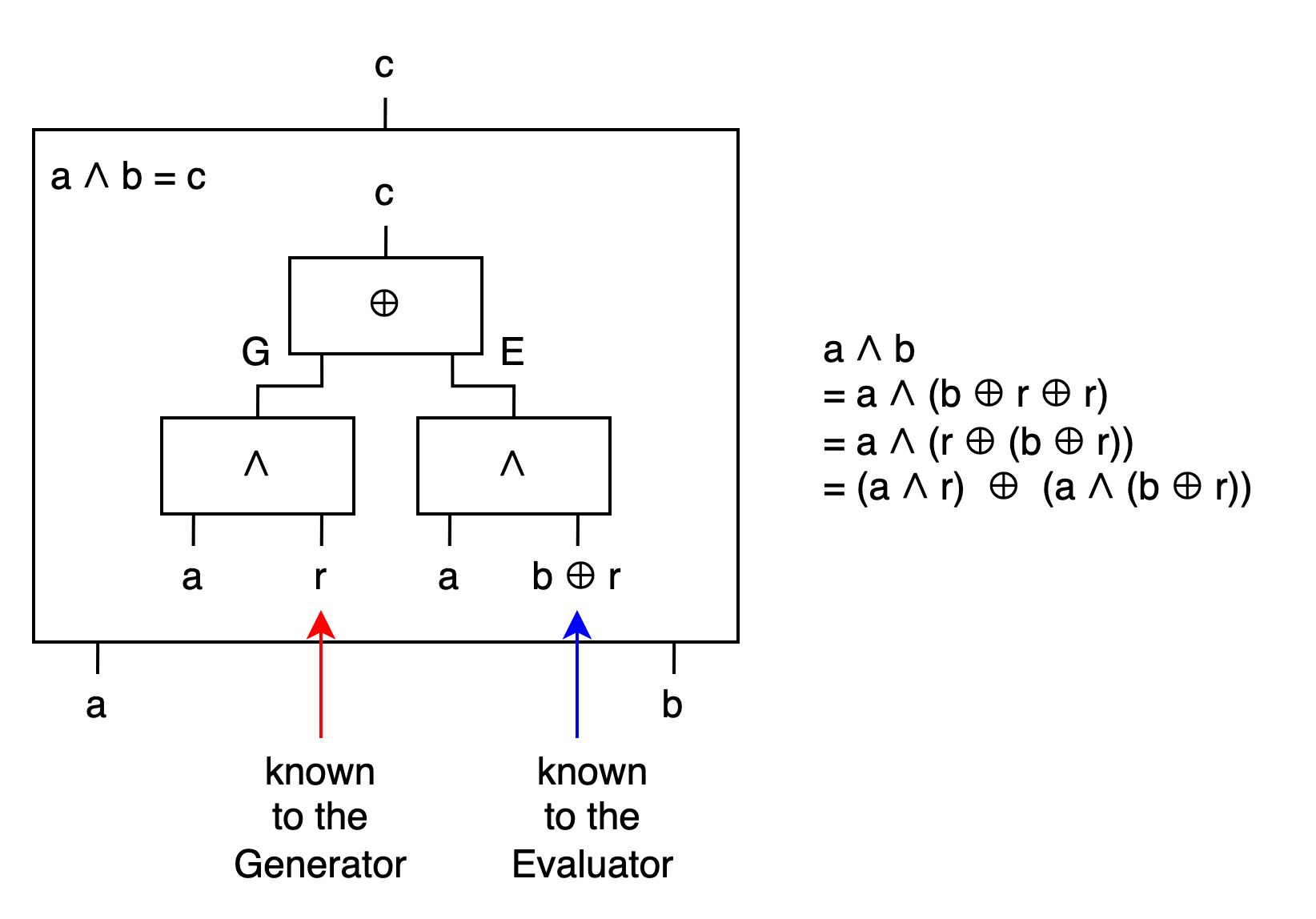
Similarly, when we only have a ∧ b, we can forcefully insert an r:
a ∧ b
= a ∧ (b ⊕ r ⊕ r)
= a ∧ (r ⊕ (b ⊕ r))
= (a ∧ r) ⊕ (a ∧ (b ⊕ r))
From the outside, it’s an XOR gate connecting two AND gates. This equation holds for any a, b, r.
We will make `r` and `b ⊕ r` known inputs later.
Clever method to create known inputs
(Reminder: The implementation of Half Gates will use Point-and-Permute, FreeXOR, and GRR3. )
Where does this r come from?
When the Generator is processing the circuit, if it encounters a ∧ b, it will use “some method” to decide a random bit r, and apply the formula above.
So for the Generator, although a and b will only have definite values during evaluation, the new AND gate (a ∧ r) has an input r that is known starting at generation time.
Since r is fixed, we only need to handle 2 * 1 instead of 2 * 2 variations.
We call G = (a ∧ r), this AND gate where Generator has a known input, the "Generator Half Gate".
Now look at the other AND gate E = (a ∧ (b ⊕ r)), called the "Evaluator Half Gate".
Since both a and b are only determined during evaluation, how can the Generator use the above technique?
The design here is special: we let the Generator reveal b ⊕ r to the Evaluator. And it’s done through the pointer bit of point-and-permute.
As introduced in the previous articles, to avoid leaking more information to the Evaluator, Garbled Circuit only lets the Evaluator know the label during the calculation process, but not the value corresponding to the label. Here, the true values of wires a and b cannot be known to the Evaluator.
But because only the Generator knows r, and it’s uniformly random, it’s okay to reveal b ⊕ r to the Evaluator, it won’t leak b. (one-time pad)
However, the Generator only knows r. Even if it wants to reveal b ⊕ r before actual execution, how does it know what value b will be when it reaches this gate?
A letter that follows the label
In movies, there’s often a plot like this: a person opens a letter, and a voice says to him:
Dear John:
When you read this letter, things should have already blah blah ...
So I blah blah ...
It’s very similar here.
The Generator writes a letter on each of the two labels of wire b. Writing on label 0:
Dear Evaluator:
When you get this label, b should already be determined.
Although I can't tell you the values of b and r in this world,
I'll tell you b ⊕ r, which is ${actual value inserted}.
Hope you can make good use of it.
Label 1 also has similar content, just with a different value for b ⊕ r.
The most intuitive implementation would be to add an extra b ⊕ r bit after each of the two labels.
But the authors of Half Gates are even more economical. These two letters each only used… 0 bits.
0 bits?
Perhaps we can look at it this way:
In Point-and-Permute, the Generator flipped a coin to decide a bit p, and attached bit p and !p to the back of keys 0 and 1 respectively.
Since p is already random, and flipping a coin is quite effortful, can we just let r = p?
If p = r = 0, then the two labels of wire b would look like:
b pointer bit b ⊕ r
key0 0 0
key1 1 1
If p = r = 1, then the two labels of wire b would look like:
b pointer bit b ⊕ r
key0 1 1
key1 0 0
We can see that in these two cases, b ⊕ r happens to have the same value as the corresponding pointer bits! So there’s no need to add an extra redundant bit, when the Evaluator gets the label, looking at the value of the last pointer bit is exactly the value of `b ⊕ r`.
Also, since the Evaluator doesn’t know whether the label in hand represents 0 or 1, seeing the pointer bit doesn’t reveal whether it’s p or !p, which means it doesn’t know whether it’s r or !r. So there’s no information leak.
Up to this point, we’ve made the Generator half gate a ∧ r have an input r that the Generator knows at generation time.
We’ve also made the Evaluator half gate a ∧ (b ⊕ r) have an input b ⊕ r that the Evaluator will know at evaluation time.
Let’s see how we can use this property to help us generate the ciphertexts for these two half gates.
Ciphertexts of the Generator Half Gate
When we encounter an AND gate a ∧ b = c, we want the Evaluator to be able to compute the output label using two input labels.
After transformation, we still want the Evaluator to be able to compute the output label c using two input labels a and b, but now it needs to go through 3 intermediate gates.
Below, I use different wire names than the book. In the book, a, b, c point to different wires during the explanation. Here, I refer to the original paper, letting the output wire of the Generator Half Gate be called wire G, the output wire of the Evaluator Half Gate be called wire E, and letting a, b, c point to fixed wires. (Please refer to the diagram above)
Below, a0 represents the label of wire a when its value is 0. a1 represents the label of wire a when its value is 1. And so on.
First, look at the Generator Half Gate G = a ∧ r
The Generator has already decided r, so
If r = 0, then G must be 0. Prepare plaintexts G0 G0.
If r = 1, then G will be determined by label a at evaluation time. a0 corresponds to G0, a1 corresponds to G1. Prepare plaintexts G0 G1.
So the Generator prepares a table having two ciphertexts like this:
if (r == 0) {
Enc(a0, G0)
Enc(a1, G0)
} else {
Enc(a0, G0)
Enc(a1, G1)
}
Permute the table by the pointer bits of label a.
When the Evaluator has label a, it can decrypt the row pointed to by label a’s pointer bit, obtaining the label of wire G.
Ciphertexts of the Evaluator Half Gate
Now look at the Evaluator Half Gate.
The Evaluator code here is not simply table lookup, but needs to run a piece of code.
At this time, the Evaluator has the label of wire a (could be a0 or a1)
Has the label of wire b (could be b0 or b1)
Has the value of b ⊕ r (from the pointer bit of wire b’s label)
We want to let the Evaluator get the correct label of E = a ∧ (b ⊕ r), and the Evaluator can only get one of E0 or E1.
The form of our ciphertext will be
Enc( one label of wire b, plaintext1)
Enc(the other label of wire b, plaintext2)
First, use different encryption keys to ensure that the evaluator can decrypt exactly one. Use b ⊕ r to determine which one to decrypt, then consider how to obtain the correct E0 or E1 from the decrypted plaintext1 or plaintext2.
case b ⊕ r = 0 (for E = a ∧ (b ⊕ r))
When b ⊕ r = 0, the entire AND is directly 0 without looking at a. We can simply let plaintext1 = E0.
But should we use b0 or b1 to encrypt / decrypt?
If b ⊕ r = 0 at evaluation time, then necessarily b == r.
Given b ⊕ r = 0, if r is 0, then the Evaluator will get b0.
Given b ⊕ r = 0, if r is 1, then the Evaluator will get b1.
So the Generator prepares the first ciphertext like this (for b ⊕ r = 0)
Enc(r == 0 ? b0 : b1, E0)
At evaluation time, if b ⊕ r = 0, use the label of wire b to decrypt this first ciphertext, and you’ll be able to obtain E0.
case b ⊕ r = 1 (for E = a ∧ (b ⊕ r))
When b ⊕ r = 1, the label of E still depends on a.
But a is unknown at generation time, so our plaintext2 is destined to be a semi-finished product, needing to interact with a’s label at evaluation time to get the right E0 or E1.
We hope to have
some_function(a0, plaintext2) = E0
some_function(a1, plaintext2) = E1
How should we design this mechanism?
This is where we’ll use the property of FreeXOR.
In FreeXOR, adding Δ to label 0 of each wire gives label 1.
So a0 ⊕ Δ = a1, E0 ⊕ Δ = E1.
So if we can add some diff to a0 to get E0, then adding the same diff to a1 will give E1!
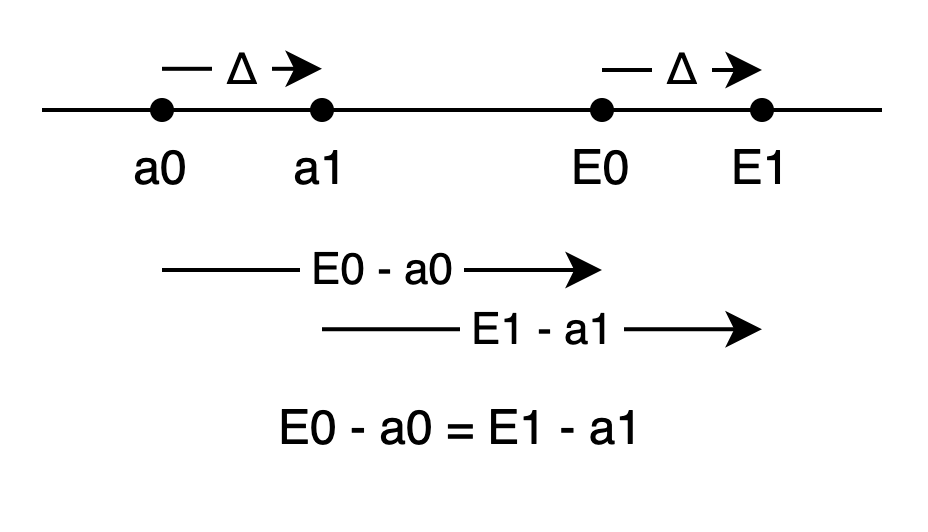
Imagine it as integers:
a0 + (E0 - a0) = E0
a1 + (E0 - a0) = E1
Written in boolean:
a0 ⊕ (E0 ⊕ a0) = E0
a1 ⊕ (E0 ⊕ a0) = E1
We let plaintext2 = E0 ⊕ a0 store this diff.
Then encrypt with “the other label of b” opposite to the case b ⊕ r = 0.
So the Generator prepares the second ciphertext like this (for b ⊕ r = 1)
Enc(r == 0 ? b1 : b0, E0 ⊕ a0)
After the Evaluator decrypts the diff, adding the diff to the label of wire a in hand will give the label of wire E.
At this point, both ciphertexts for the Evaluator Half Gate are prepared. They can be output in order, without permutation. Each case uses one ciphertext.
How does the Evaluator Half Gate compute?
If you fully understand the two cases of b ⊕ r, the Evaluator’s code should look like this:
function compuateEvaluatorGate(eCiphertext1, eCiphertext2, aLabel, bLabel) {
let b_XOR_r = pointerBitOf(bLabel);
if (b_XOR_r == 0) {
return decrypt(bLabel, eCiphertext1);
} else {
let diff = decrypt(bLabel, eCiphtertext2);
return xor(aLabel, diff);
}
}
Harvest
We’ve created two ciphertexts for the Generator Half Gate:
Enc(a0, G0)
Enc(a1, r == 0 ? G0 : G1)
We’ve also created two ciphertexts for the Evaluator Half Gate:
Enc(r == 0 ? b0 : b1, E0)
Enc(r == 0 ? b1 : b0, E0 ⊕ a0)
We have 4 ciphertexts. But by choosing G0 and E0, we can make the first entries in these two groups of ciphertexts become 0s. This way, we only need to transmit the latter two. (GRR3 technique)
The final XOR gate is computed. FreeXOR doesn’t need ciphertexts.
So the entire AND gate c = a ∧ b only needs two ciphertexts in total. And it’s compatible with FreeXOR.
Job done!
Postscript:
I feel that the book hides some details in the Evaluator Gate part (like b ⊕ r has no wire and thus no label). These details can be supplemented through Fig 1 and Fig 2 of the original paper.
The author of the book, Mike Rosulek, gave a lecture at Simons Institute in 2015, which is very good to watch!
At 47:35, someone asked:
“do you have any idea roughly how many gates you will actually be in the position where you know one of your inputs / so obviously the input gates you know what your inputs are / but after that how far can you propagate it normally”
This person had the same question as I did at the beginning :-)