Malicious Secret Sharing - Authenticated Secret Sharing
BDOZ
在 semi-honest 的情況下, 每個 party 各自持有某個 variable 的 shares.
比方說 P1 P2 P3 持有以下的 additive shares:
var10 6
P1 2
P2 3
P3 1
當我們要 reconstruct 出 “var10 = 6” 的時候, 只要每個 party 把自己的 share 公開再相加就好.
但是在 malicious 的情境中, P2 怎麼知道當 P1 說 “我的 var10 的 share 是 2” 的時候, P1 的 share 就真的是 2 呢?
在 BDOZ 中, 每個 variable 除了拆成 shares 之外, 還對每個 variable 加上了 party 之間一對一的 key 與 MAC. (一開始從 offline protocol 得來的, 後面再逐步推導)
當 P1 要和 P2 說 “我的 var10 的 share 是 2” 的時候, 還要附上 var10 的 P1-to-P2 的 MAC. 而 P2 收到之後, 會用 var10 的 P1-to-P2 的 key 來 verify. 如果 P2 計算 MAC(2, var10-key-P1-to-P2) = var10-MAC-P1-to-P2 等式成立, 則 P2 願意相信 P1 沒有作弊.
var10 6 For sending For verifying
P1 2 var10-MAC-P1-to-P2 var10-MAC-P1-to-P3 var10-key-P2-to-P1 var10-key-P3-to-P1
P2 3 var10-MAC-P2-to-P1 var10-MAC-P2-to-P3 var10-key-P1-to-P2 var10-key-P3-to-P2
P3 1 var10-MAC-P3-to-P1 var10-MAC-P3-to-P2 var10-key-P1-to-P3 var10-key-P2-to-P3
所以當我們有 n 個 party 時, 對於每個 variable, 我們都要有 O(n^2) 個 key 和 MAC 來確保正確性.
這些 key / MAC 不僅對一個 value 的 shares 有效, 而且還要能隨著計算更新.
舉例來說, 如果 F(x, y) = ((x * y) + x) * y, 想計算 f(6, 4) 大概會像這樣:
let var10 = 6 // only known by P1 (with keys / MACs)
let var20 = 4 // only known by P2 (with keys / MACs)
let var30 = var10 * var20 // secret value (with new keys / MACs)
let var40 = var30 + var10 // secret value (with new keys / MACs)
let var50 = var40 * var20 // open and verify
一個 honest party 如果照著 protocol 計算出 var30 var40 var50 的 keys, 則每一步的 keys 都讓他能抵擋來自 dishonest party 的訊息.
Offline / Online
和前面介紹的 Beaver triple 一樣, BDOZ 分成 offline 和 online 的 phases.
P1 P2 P3 先用 offline phase 的 protocol 製造出很多 “single”s 和 “triple”s. 這個過程和 online 的 input 無關, 甚至也和 online 要計算的 function 無關.
到 online phase 時, 先取來 2 組 singles, 讓它變成 input 的值 (var10 = 6, var20 = 4). 在乘法時取用 triples. 每一步都計算正確的 keys / MACs. 最後再 open output variable var50 並檢查正確性.
SPDZ
BDOZ 中, n 個 party 一對一的互相 verify, 總共需要另外儲存 O(n^2) 個數字.
SPDZ 改成是所有 party 一起 verify. 每個 variable 每個 party 只要另存一個數字, 總共只要 O(n) 個數字.
最後 open 一個 variable 需要三個步驟: open shares / commit to diffs / open diffs. 這裡 dishonest party 很難讓假的 value 通過驗證. (等於要猜中 honest party 手中的 diff 才行)
A SPDZ Example
以下我們用 mod 7 的 field 為例.
SPDZ 中, 有一個 global 的 delta, 由每個 party 各持有一份 share.
每個 party 只知道自己的 share, 但不知道 delta 是多少.
假設 delta 是 6.
假設 P1 P2 P3 各持有 d1 = 2, d2 = 3, d3 = 1.
在每個 variable x 的 shares 中, 每個 party 另外持有一個 t = delta * x 的 share.
每個 party 只知道自己的 share, 但不知道 x 和 t 是多少.
假設 x 是 2. 則 t = delta * x = 6 * 2 = 12 = 5 mod 7 .
假設 P1 P2 P3 各持有 x1 = 5, x2 = 1, x3 = 3 以及 t1 = 3, t2 = 5, t3 = 4 .
現在我們試著 reconstruct x.
每個 party 先 publish 自己的 x 的 shares: x1 = 5, x2 = 1, x3 = 3 .
每個 party 可以各自 reconstruct 出 x = (5 + 1 + 3) mod 7 = 2 mod 7 .
但是我們不知道有沒有人作弊.
所以接著要 P1 publish 手上的 d1 * x - t1 的 commitment.
所以接著要 P2 publish 手上的 d2 * x - t2 的 commitment.
所以接著要 P3 publish 手上的 d3 * x - t3 的 commitment.
我們觀察上面減號的兩邊. 左邊加在一起可以湊出 (d1+d2+d3) * x = delta * x, 右邊是湊出 t 也是 delta * x . 如果沒有人作弊的話, 這三個 diff 加起來應該是 0.
接著要三個 party open 這三個數字.
d1 * x - t1 = 2 * 2 - 3 = 1
d2 * x - t2 = 3 * 2 - 5 = 1
d3 * x - t3 = 1 * 2 - 4 = -2
加在一起的確是 0.
這三個數字不會洩漏 d1 d2 d3, 也不會洩漏 t1 t2 t3. 也都不會洩漏 delta.
先 commit 再 open 是怕最後一個人看到前面的數字才湊成 0. 先 commit 可以避免這個問題.
假設 P2 P3 共謀, 想要欺騙 P1 x 是 3. 但 P2 P3 完全不知道 d1 t1 是多少, 因此很難去 cancel 3 * d1 - t1 的值. 也就騙不了 P1.
我們也可以想成: 為了保護 x 拆出的 x1 x2 x3 不被更改, 有個 trusted party 弄出了 delta 和 delta * x. Trusted party 用兩種方法拆解 delta * x : 一種是拆 x, 一種是拆整個 delta * x. 這兩個方法拼起來的值應該要一樣. 而檢查是否一樣的方法並不是把兩個方向各自完整的 reconstruct 再比較(因為這樣會洩密), 而是看總 diff 是否為 0.
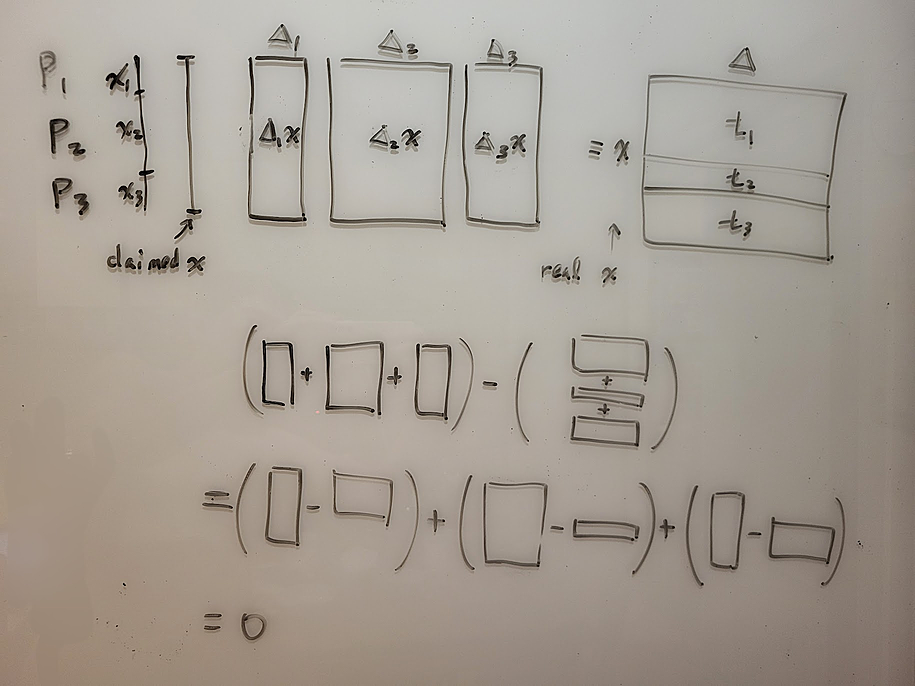
又, 如果 open 的過程只對單一個 party (比方說 P1) 送訊息, 則可以只讓 P1 知道實際的 value, 而其他 party 保持不知道.
計算
以下繼續用 mod 7 的 field.
delta = 6 = d1 + d2 + d3 = 2 + 3 + 1
如果 P1 P2 P3 有著 [2].
x delta * x
2 6 * 2
P1 5 3
P2 1 5
P3 3 4
我們希望可以作一些運算, 且仍然保持可以 verify 的性質.
x * c
先看怎麼把原來的 shares “* c” . (c 是 public constant)
2c 6 * 2c
P1 5c 3c
P2 1c 5c
P3 3c 4c
這樣就得到了一份可 verify 的 [2 * c] .
x + c
再看怎麼把原來的 shares “+ c” .
delta * (x + c) = (delta * x) + (delta * c)
2+c 6 * (2+c)
P1 5+c 3 + 2c <- (t1 + d1 * c)
P2 1 5 + 3c <- (t2 + d2 * c)
P3 3 4 + 1c <- (t3 + d3 * c)
這樣就得到了一份可 verify 的 [2 + c] .
x + y
如果
x delta * x y delta * y
2 6 * 2 3 6 * 3
P1 5 3 4 2
P2 1 5 5 1
P3 3 4 1 1
想計算 x + y 的話, 可以把對應的數字加起來:
x + y delta * (x + y)
2 + 3 = 5 6 * 2 + 6 * 3 = 2
P1 5 + 4 = 2 3 + 2 = 5
P2 1 + 5 = 6 5 + 1 = 6
P3 3 + 1 = 4 4 + 1 = 5
這樣就得到了一份可 verify 的 [x + y] .
x * y
想計算 x * y 需要 Beaver triple. 假設拿到一組事先準備好的 a * b = c .
P1 P2 P3 不知道 a b c 這三個數字.
x = a + d
y = b + e
x * y = (a + d) * (b + e)
= ab + ae + db + de
= c + ae + db + de
let var1 = x
let var2 = y
let var3 = a
let var4 = b
let var5 = c
let var6 = d = x - a = var1 - var3
open var6
let var7 = e = y - b = var2 - var4
open var7
let var8 = ae = var3 * constant var7
let var9 = db = constant var6 * var4
let var10 = de = constant var6 * constant var7
let var11 = x * y
= c + ae + db + de
= var5 + var8 + var9 + constant var10
這樣就得到了一份可 verify 的 [x * y] .
初始化 Input
假設已經有拿到一個 single “v” 在 var1.
現在希望 P1 可以把自己的 input x 輸入到 var2.
我們希望只有 P1 知道 var2 的 value, 其他 party 不知道.
我們希望 var2 有著可以被 SPDZ verify 的格式.
一開始所有 party 對 P1 open var1 = v.
P1 計算出 constant “x - v”, publish x - v, 要求大家計算 var2 = var1 + (x - v) .
這樣 var2 便是符合條件的 variable.
尾聲
BDOZ 和 SPDZ 都是多準備一些額外的數字, 讓 dishonest party 會被擋下. Honest party 只要只要一步一步的計算對應的數字, 就能 verify 最後正確的 output.
SPDZ 的 paper 中用 somewhat homomorphic encryption (SHE) 的方式生成符合 SPDZ 格式的 shares. 後來 Keller et al. 提出了 MASCOT 來加速 offline phase. 之後 Keller et al. 又提出基於 SHE 的 Overdrive 來改進 offline phase. 實作可以參考 MP-SPDZ 的 repository.