OT Extension (IKNP)
Bob: Hi Alice.
Alice: Hi Bob. What would you like to discuss today?
Bob: After seeing Oblivious Transfer in Garbled Circuit last time, I looked up some more information. I came across an interesting thing called IKNP OT Extension and wanted to discuss it with you.
Alice: Sure, let me look up some information as well…
Alice: Alright. Do you remember the OT we discussed last time?
Bob: Yes, I do. It’s where you have two messages, and if I choose 0, I see message0, and if I choose 1, I see message1. But I can’t see your other message, and you don’t know which message I chose to look at.
Alice: So what do you think OT Extension is doing?
Bob: If you have 1 million pairs of messages for me to choose from, we’d have to perform OT 1 million times, which is quite costly.
Some people called IKNP thought: Is it possible to do, say, 100 OTs, plus some additional design, to achieve the effect of the original 1 million OTs?
Shall we roleplay the characters inside to check our understanding?
Alice: Okay. I’ll be Alice… I mean, I’ll be the Sender, and you be the Receiver.
Bob: OK. Let’s not look at 1 million pairs of messages first, let’s just look at one pair.
As the receiver, I use a secret bit r to represent which message I want. And T represents a random bit string I generate.
If I have a way to
- use r to control whether T appears in position 0 or position 1 on your side
- and put a bit string I don’t know in the other empty position
Then we can use it for OT: As long as you encrypt the messages with the corresponding bit strings and send them to me, I can only uniquely decrypt the one encrypted with T – which is the message pointed to by r.
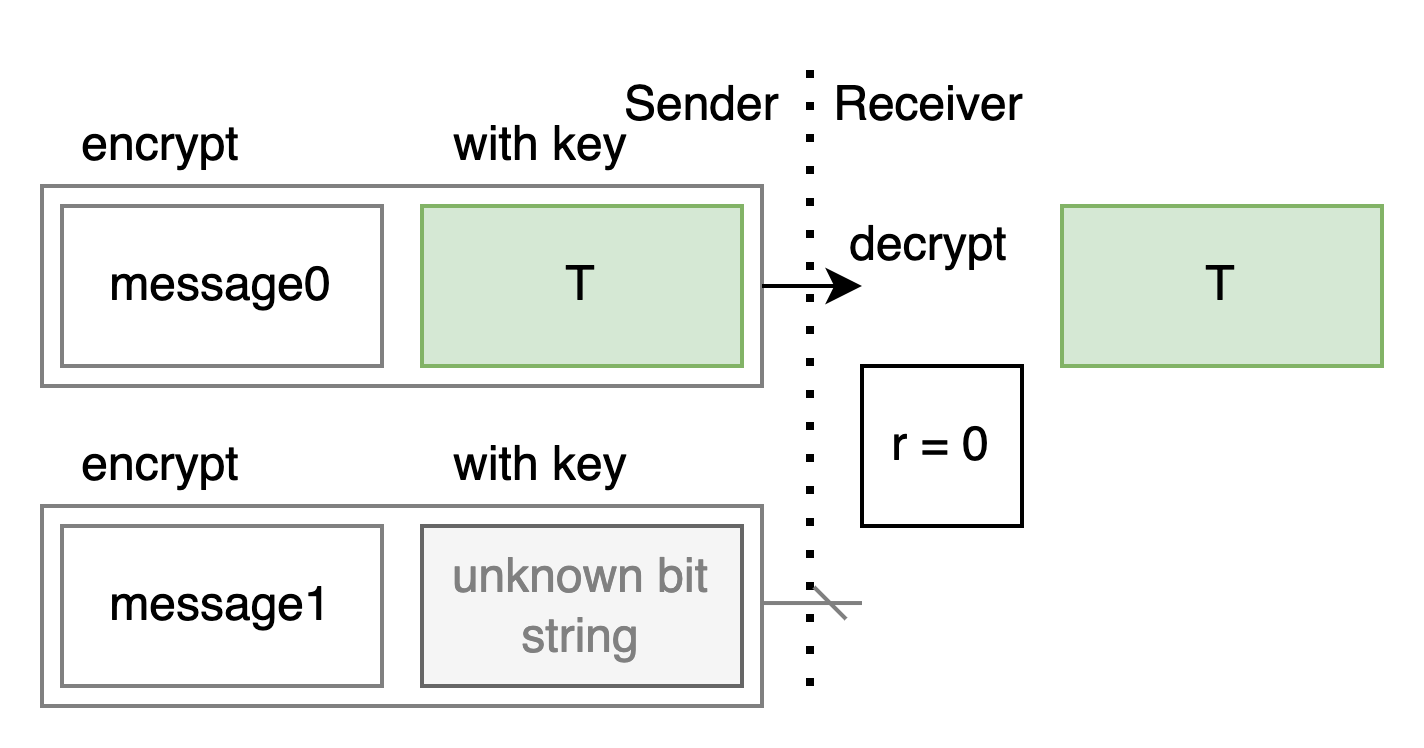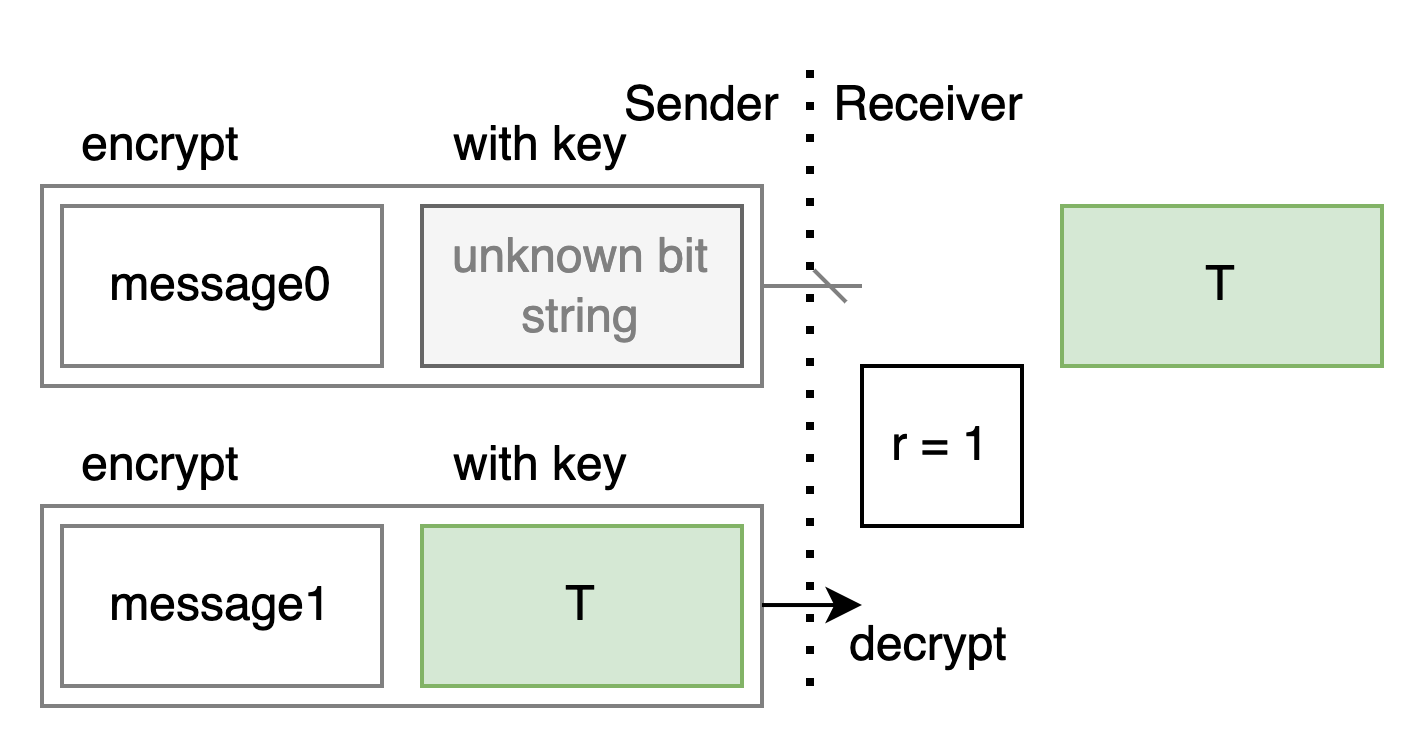
Alice: Let’s simplify it further, let’s first shrink T to just one bit.
As the sender, I generate a secret random bit s.
Because you don’t know s, you shouldn’t know T⊕s either.
If I could calculate T⊕s, I could use it as the unknown bit you don’t know to put in the other box.
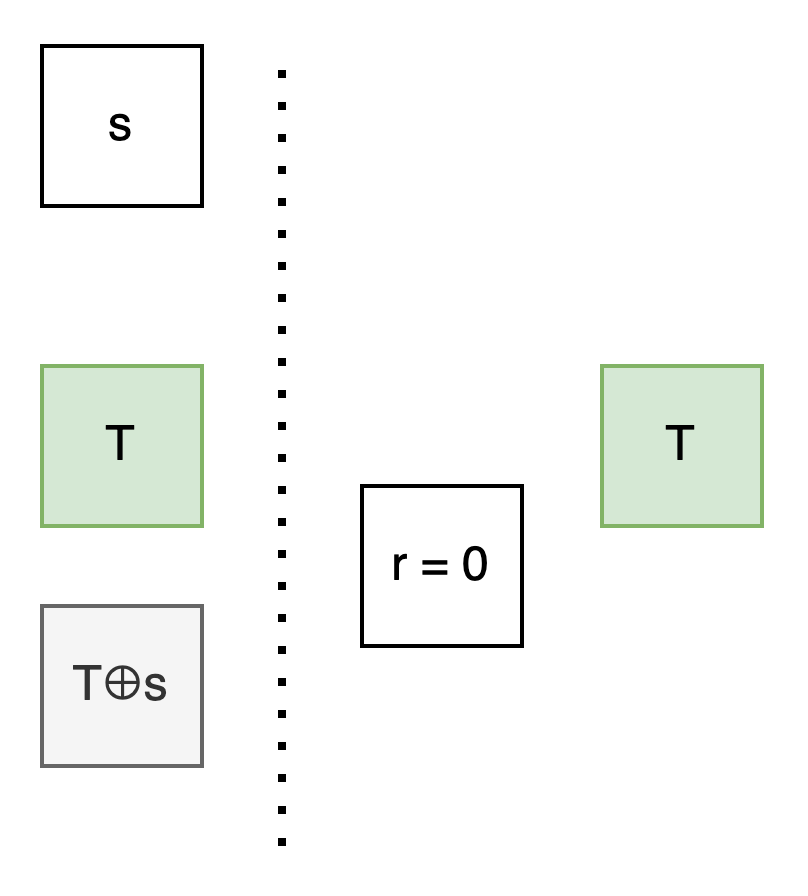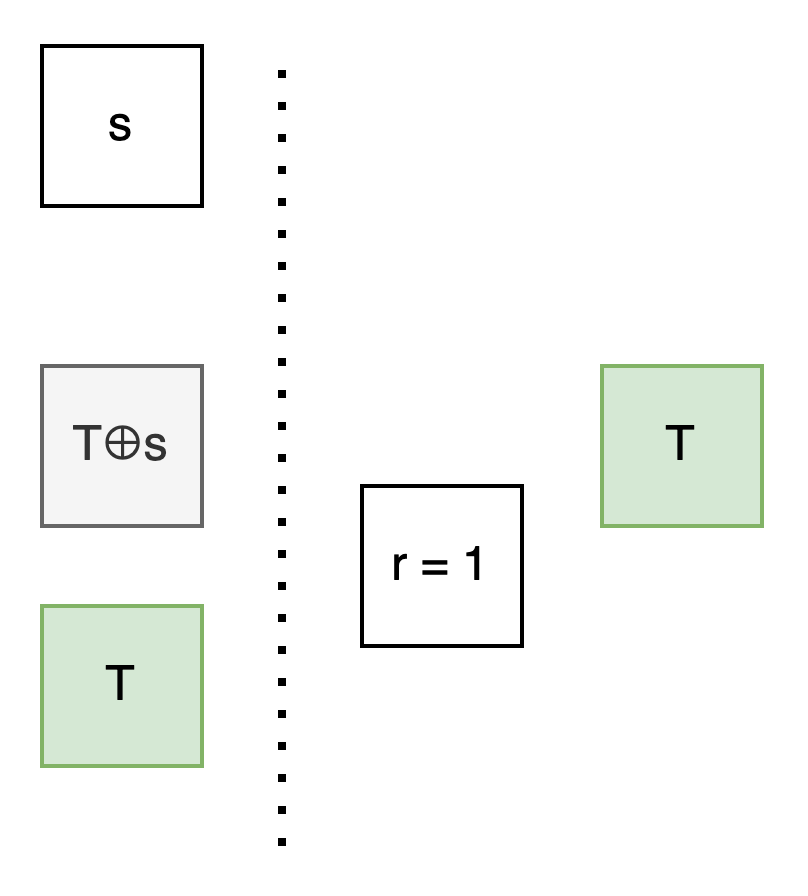
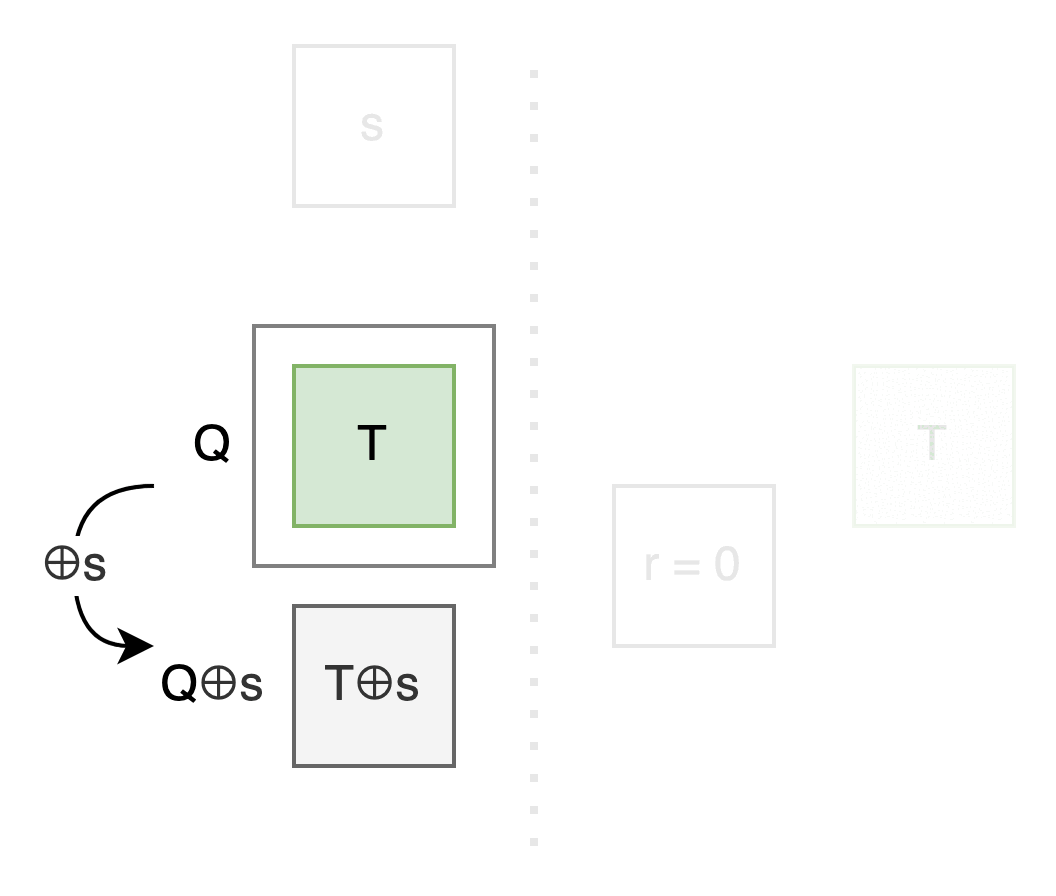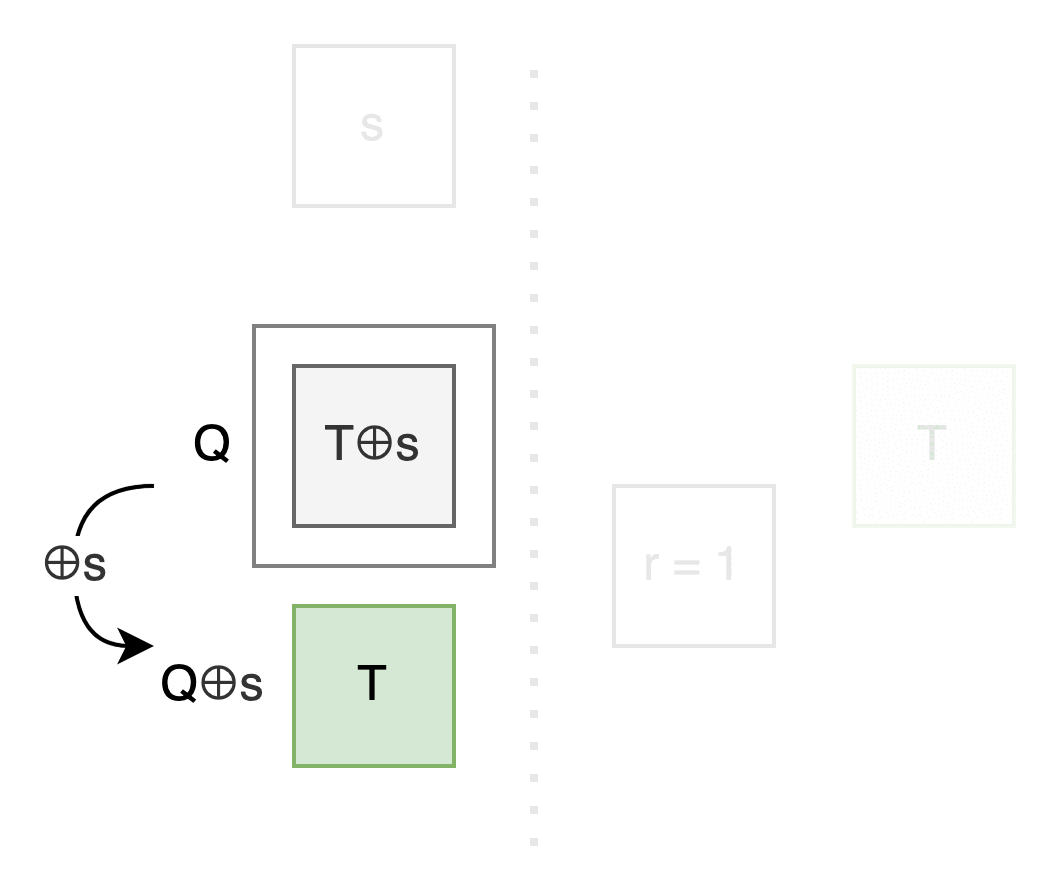
Let’s observe the relationship between the upper and lower boxes: No matter if r is 0 or 1, the upper box ⊕s always gives the lower box.
If we name the upper box Q, then the lower box is Q⊕s.
We can transform the original problem to: Focus on Q, see how to use r to control whether T or T⊕s appears in that box.
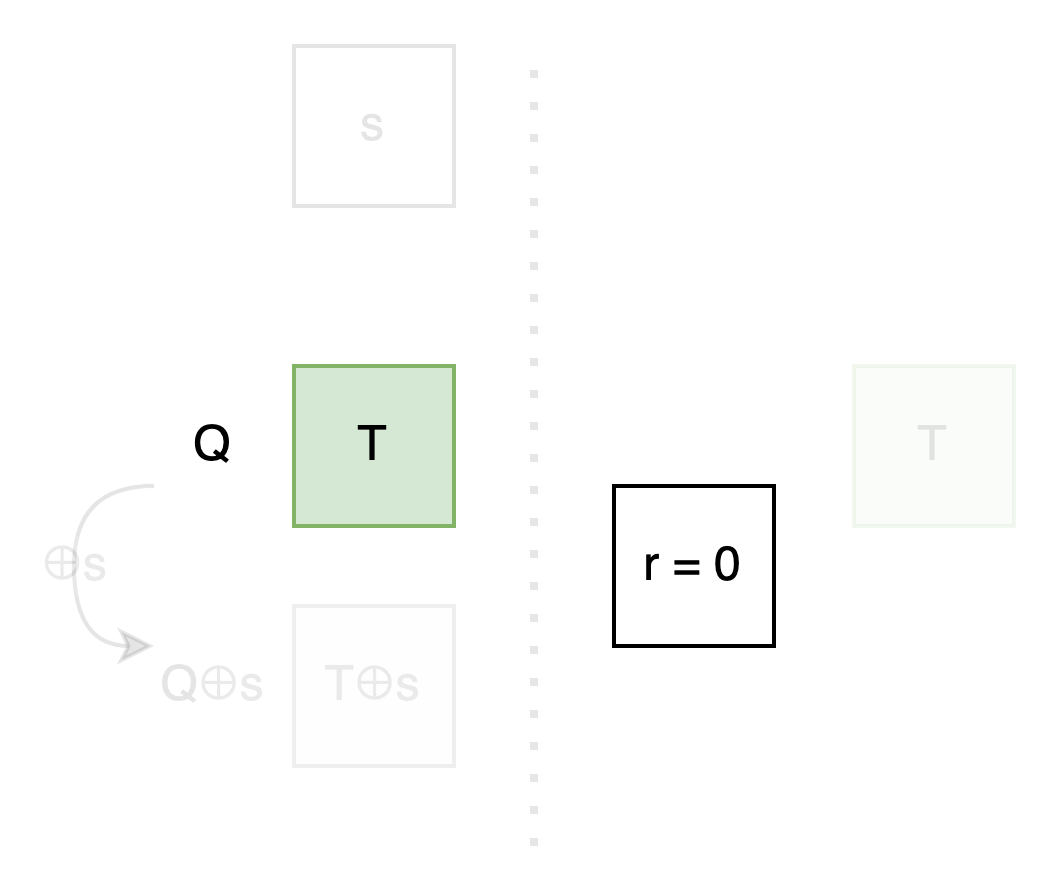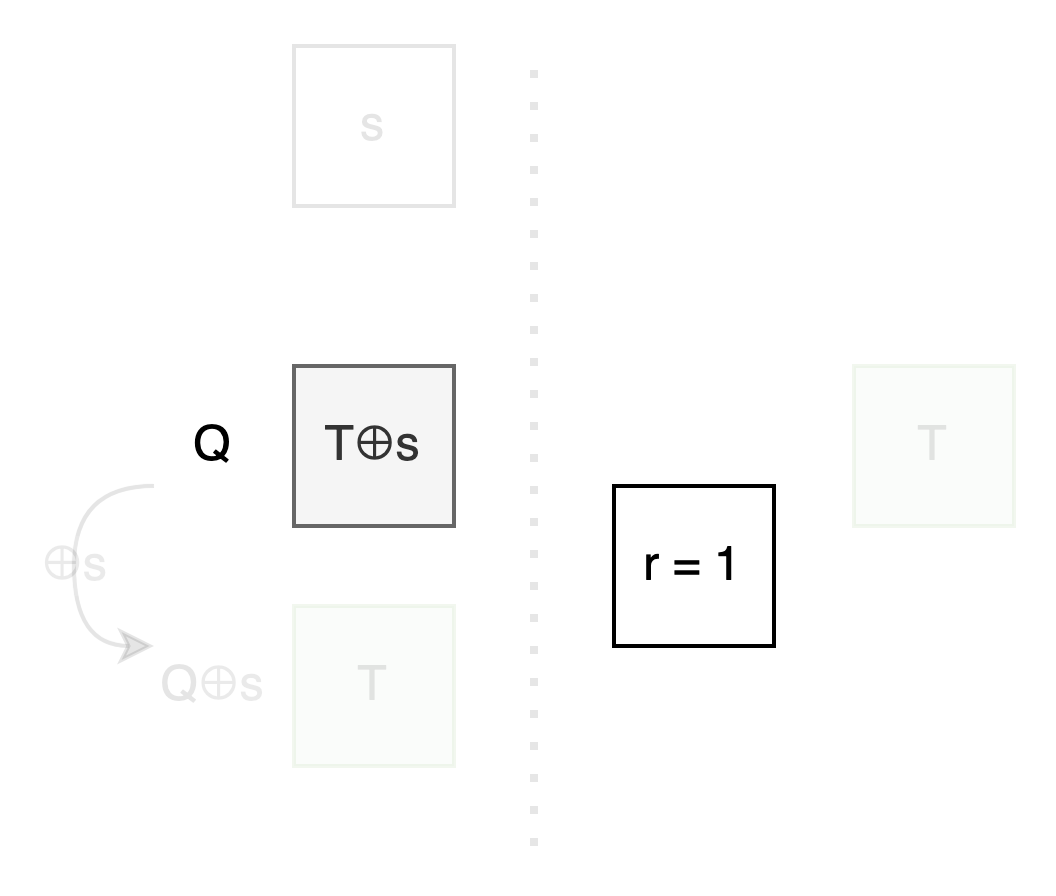
Bob: To summarize: We’ve just reduced from 1 million pairs of messages to one pair, from two bit strings to two bits, then focused on how the upper bit Q is controlled by r to be T or T⊕s, so Q⊕s will be the reverse, T⊕s or T. As long as you encrypt the messages with Q and Q⊕s and send them to me, I can only open the message where T is, thus achieving OT.
But then again, you can’t know my r and T, and I can’t know your s.
Alice: Yes. If I explicitly know whether I have T or T⊕s, then I would know r, which would violate the requirements of OT.
Bob: Conversely, if I know your s, I could decrypt both messages encrypted with T and T⊕s, which would also violate the requirements of OT.
So how can we make you calculate:
Q = T if r = 0
Q = T⊕s if r = 1
in a situation where I don’t know s and you don’t know r? It’s done by…
Alice: Waiting for you to say it…
Bob: Let’s say it together…
Alice, Bob: Reverse OT!
Alice: (That’s so childish…) Let’s go back to reverse OT.
Bob: Reverse OT.
That is, I temporarily act as the sender, and you temporarily act as the receiver.
Regardless of whether r is 0 or 1, I prepare two boxes for you to choose with s, but the contents of the boxes will change according to r.
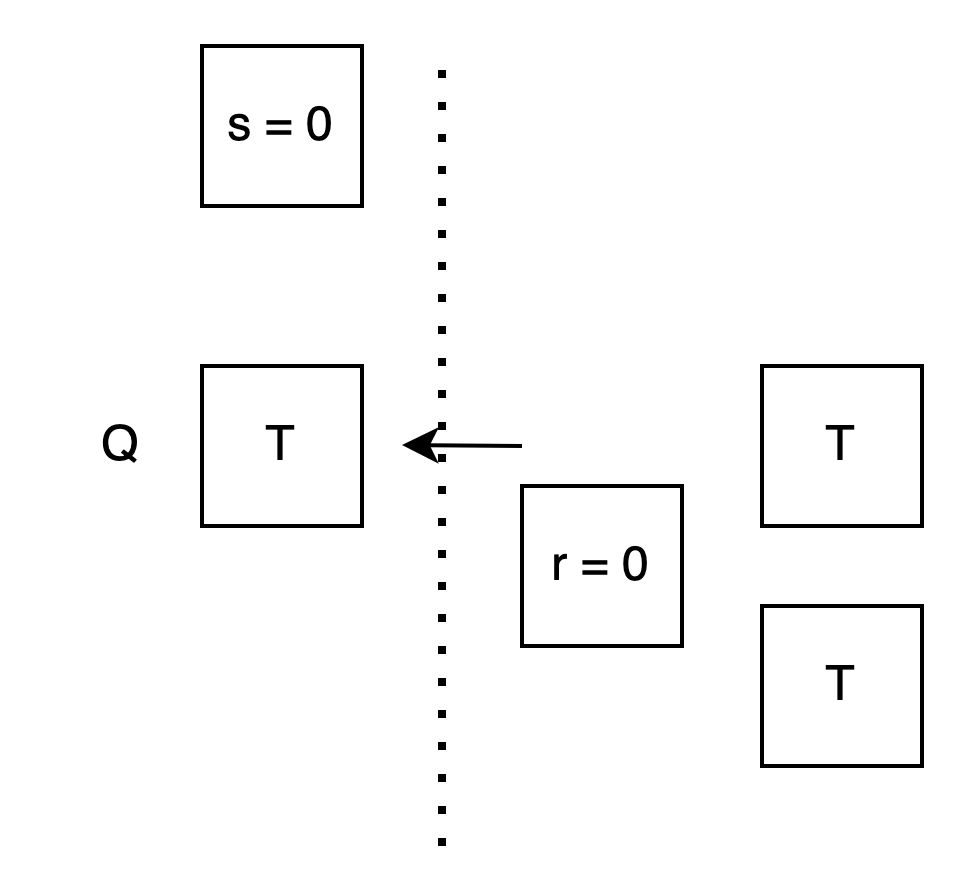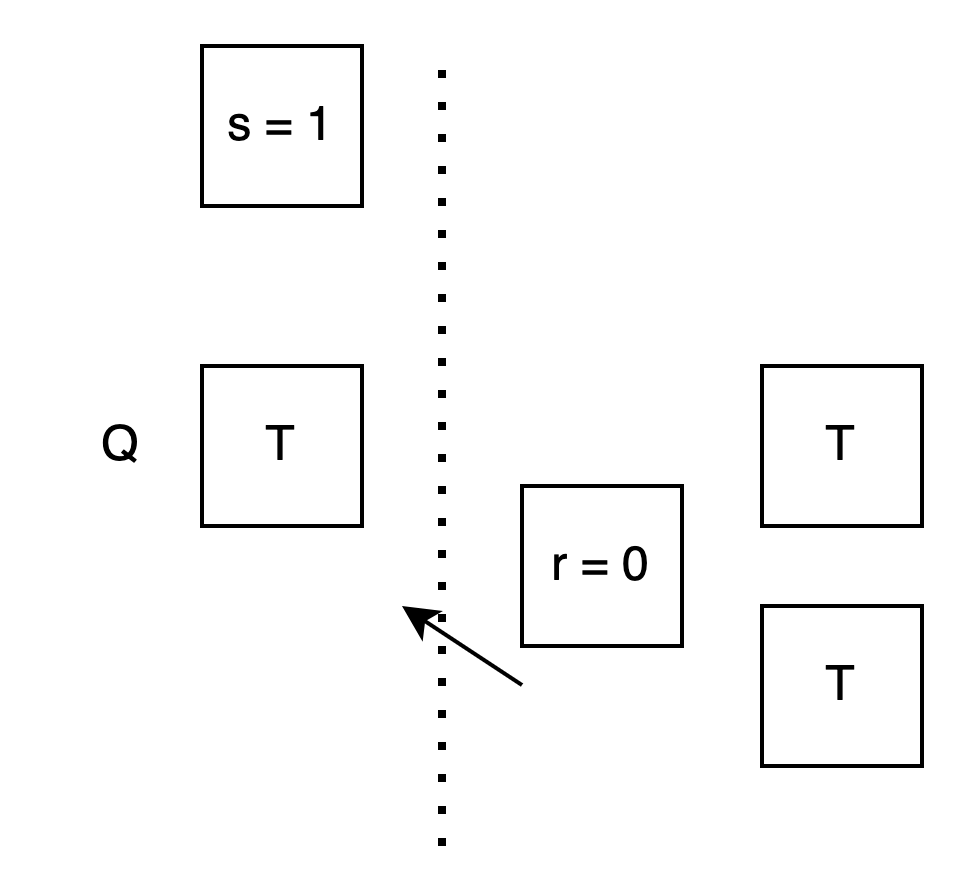
First, look at the case r = 0: I want you to calculate T, so I prepare two boxes, both containing T.
Alice: I choose a box using s. Whether I choose 0 or 1, because the contents are the same, I will definitely get T.
Bob: Now look at the case r = 1: I want you to calculate T⊕s. But I don’t know s. So I think:
Assuming you’ll pick the 0th box when s is 0, so I first put T⊕s = T⊕0 = T in the 0th box.
Assuming you’ll pick the 1st box when s is 1, so I first put T⊕s = T⊕1 = NOT T in the 1st box.
Alice: This way, when I use the value of s to choose a box, whether I choose the 0th or the 1st, the content will be exactly T⊕s!
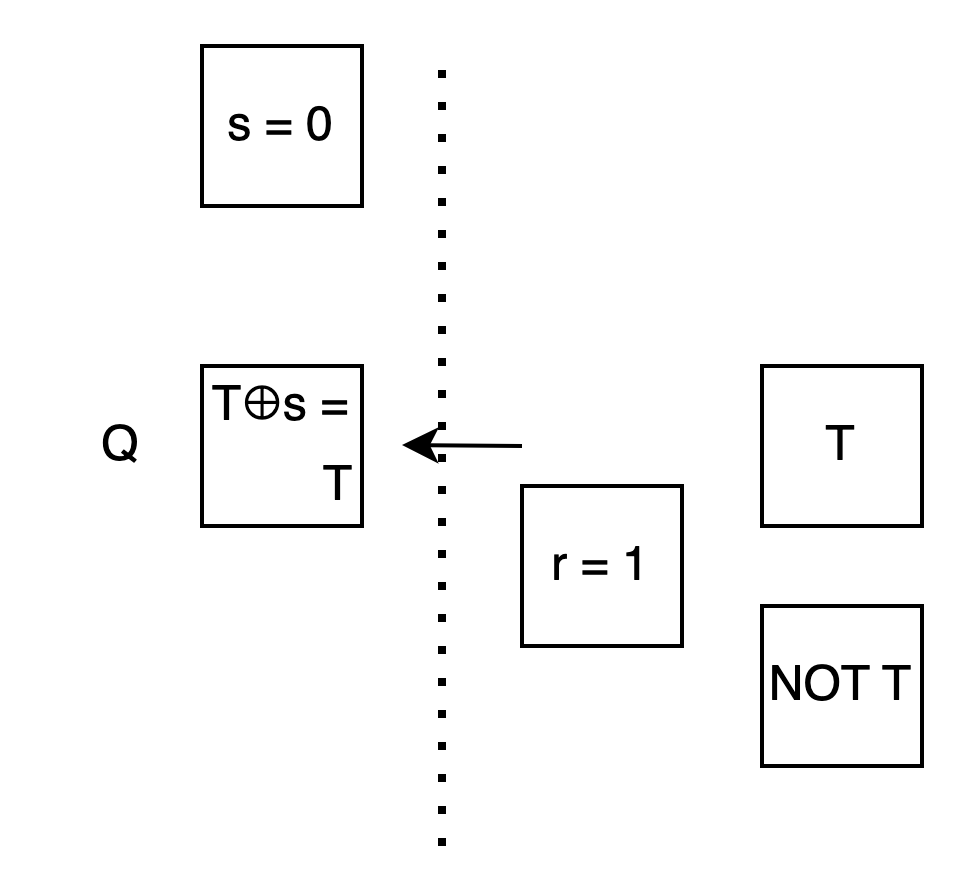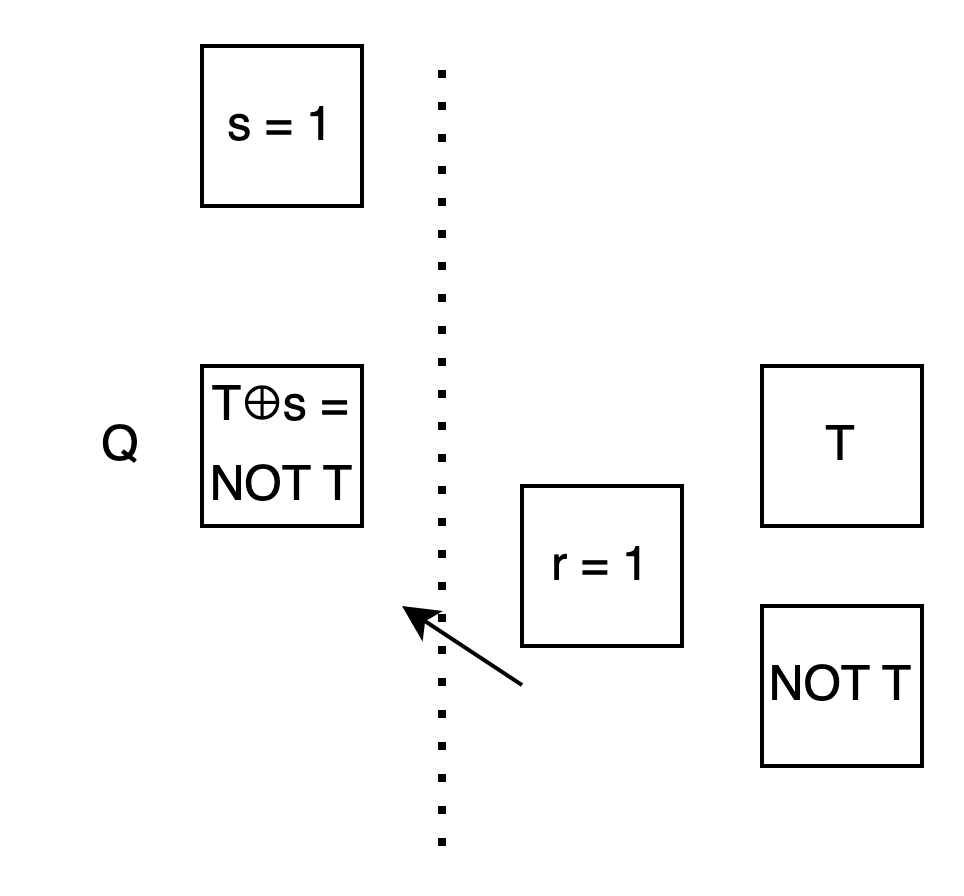
Bob: For you, the actions in these two cases are the same, which is using the value of s for reverse OT.
Alice: Although it seems like I made a choice using s, whether I calculate T or T⊕s is still based on your choice of r.
Bob: It’s “our” choice.
Alice: Also, just like the two values on my side can always be represented as Q and Q⊕s, the values on your side can always be represented as T and T⊕r.
Bob: Yes. It’s also more convenient to call them this way.
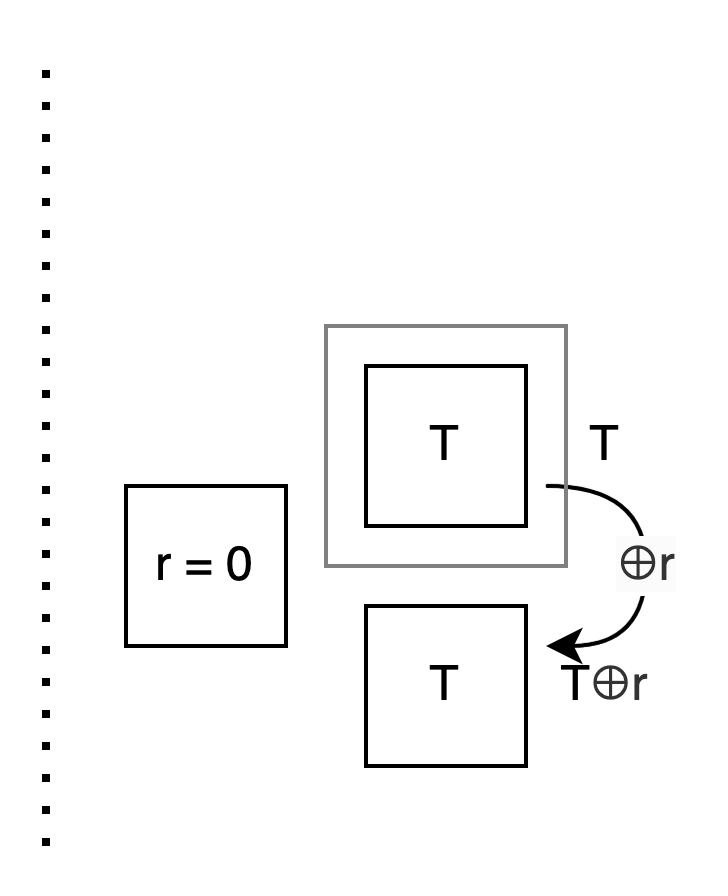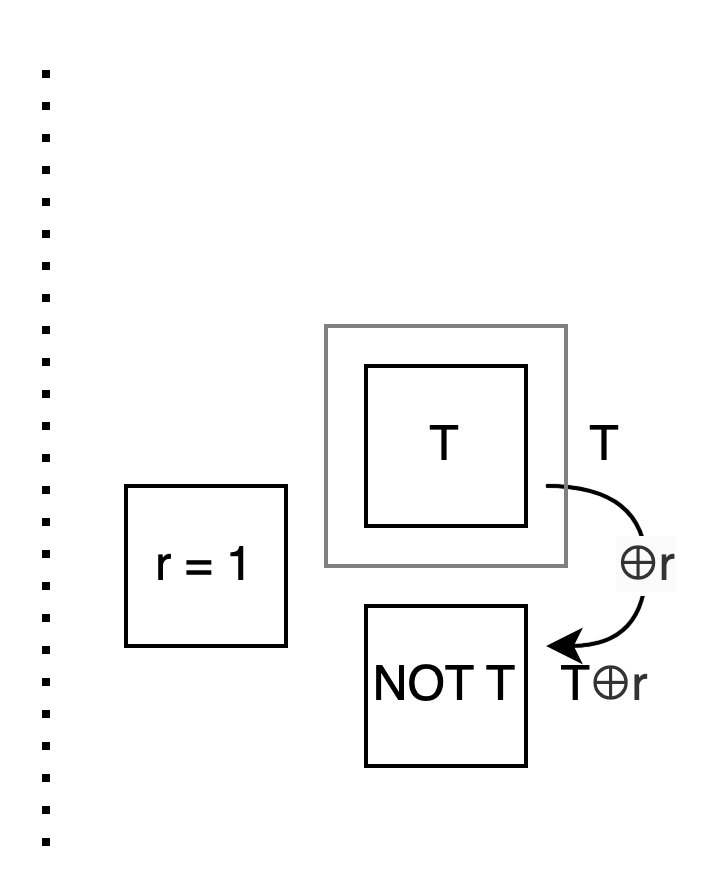
Alice: We’ve covered the core part pretty well. Let’s summarize.
Bob: Okay. Initially, I want to receive message0 or message1 from you, and I use this bit r to specify.
I first randomly generate a bit T that you don’t know and put it in the upper box, then calculate T⊕r and put it in the lower box.
Alice: Then I randomly generate a bit s that you don’t know. I use s to do a reverse OT with you.
Although I don’t know your r, the effect is that I will get T or T⊕s depending on r. I put the result in the upper box Q.
Then I calculate Q⊕s and put it in the lower box. This way, the two boxes will be (T, T⊕s) or (T⊕s, T).
I use them to encrypt message0 and message1 respectively and send them to you.
Bob: Although I know T, I don’t know T⊕s, so I can only decrypt one of them, which is the message encrypted with T, controlled by the position of r.
Alice: Let me write a program…
Alice: Alright, it’s like this. The left side is me, the right side is you. Black is 0, white is 1:
Alice: Phew, after all this talk, we’ve only transmitted one pair of messages. And using 1 bit for encryption is not secure at all.
Bob: We need to use more bits for encryption.
Alice: That means your T and my s need to become longer, we need to do OT multiple times, like this:
Bob: Because the entire T⊕r is prepared using the same bit r, it will be either entirely the same as or entirely opposite to T. This way, after you do OT several times, Q will also be either an entire T or an entire T⊕s.
Alice: Then I take the entire Q and ⊕s, so (Q, Q⊕s) will be two lines of (T, T⊕s) or (T⊕s, T), which can safely encrypt a pair of messages.
Bob: Now comes the crucial final step. Let’s see how to use these few OTs to achieve the effect of the original large number of OTs.
Alice: Let’s look at the program first, it’s like this:
Bob: Here, for each r, I generate corresponding T and T⊕r. Because each layer uses the same s for selection, you can use s to vertically select an entire column each time.
Alice: Because the T and T⊕r you prepare for each layer are based on the r of that layer, and Q is also my reverse OT result with s, so each layer is also (T, T⊕s) or (T⊕s, T).
Bob: Yes, I’ve checked each layer, and T does appear in the position pointed to by r.
Alice: Although we only performed a small number of OTs, because we selected a large number of vertical bits each time, we quickly filled up Q and Q⊕s.
This way, the two messages of each layer can be encrypted with (T, T⊕s) or (T⊕s, T) and sent to you, and a large number of OTs are completed!
Bob: Phew! Thank you for discussing this with me, I feel like I understand it even better now!
Alice: Thank you too! See you next time!
