Permutation Network
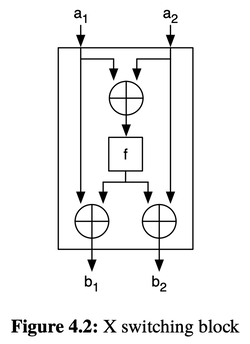
Conditional Swapper (X Switching Block)
Some common functionalities can be optimized through handwritten circuits. The conditional swapper is one such example.
The desired functionality is as follows: use a control bit p to determine whether to swap a1 and a2:
if (p) {
b1 = a2 // swap
b2 = a1
} else {
b1 = a1 // do nothing
b2 = a2
}
The swap branch can be thought of as canceling out the original and adding the desired:
b1 = a1 XOR a1 XOR a2 // b1 = a1 - a1 + a2
b2 = a2 XOR a2 XOR a1 // b2 = a2 - a2 + a1
However, circuits don’t have “if” statements, so we need to merge the two branches.
Only modify when p = true. Otherwise, let the original value XOR with 0, which doesn’t change it.
b1 = a1 XOR (p AND (a1 XOR a2))
b2 = a2 XOR (p AND (a2 XOR a1))
The last two terms are the same, so they can be shared.
So we arrive at Figure 4.2 in the book. Use p to control whether to swap. (f = p AND (a1 XOR a2))
Garbled Circuit
Let’s look at this swapper from a Garbled Circuit perspective.
If we apply FreeXOR, then this circuit only has the cost of one AND gate.
If in certain scenarios the control bit p is known, we can apply half gate, requiring only one ciphertext.
Waksman Network
We can also look at the swapper above from the perspective of a permutation network.
If we have inputs a1 a2, the possible permutations are a1 a2 and a2 a1.
Can we have a circuit that arranges the inputs into any permutation we want?
Yes, we can.
If we set the Swapper’s control bit to 0, it will produce the permutation a1 a2.
If we set the Swapper’s control bit to 1, it will produce the permutation a2 a1.
What if we have more than 2 inputs?
The Waksman Network is a type of permutation network.
For n inputs, it only needs O(n log n) swappers to create any specified permutation.
Here we’ll look at the case where n is a power of 2. How to go from 2 to 4, from 4 to 8, and so on.
For example, suppose we have a Waksman network with 4 inputs that can handle all 4! permutations. Using this 4-input network as a base, how can we expand it to handle 8 inputs?
The method is as shown in the original paper’s Fig. 3:
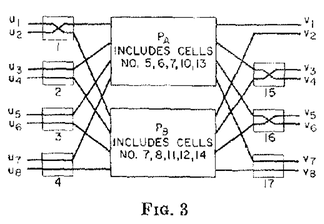
Place two 4-input networks in the middle, and put 2-input networks for every two inputs and every two outputs on the sides. The top right one can be omitted.
Connect the top of the side 2-input networks to the top of the middle 4-input networks, and the bottom to the bottom.
Then start from the top right, move from right to left, from left to right, until a cycle is formed.
Repeat the above steps until all cycles are completed.
It’s recommended to manually calculate using the example from the original paper. (The “constructive proof” section)
1 2 3 4 5 6 7 8
2 7 6 8 4 3 1 5
I made a short video:
