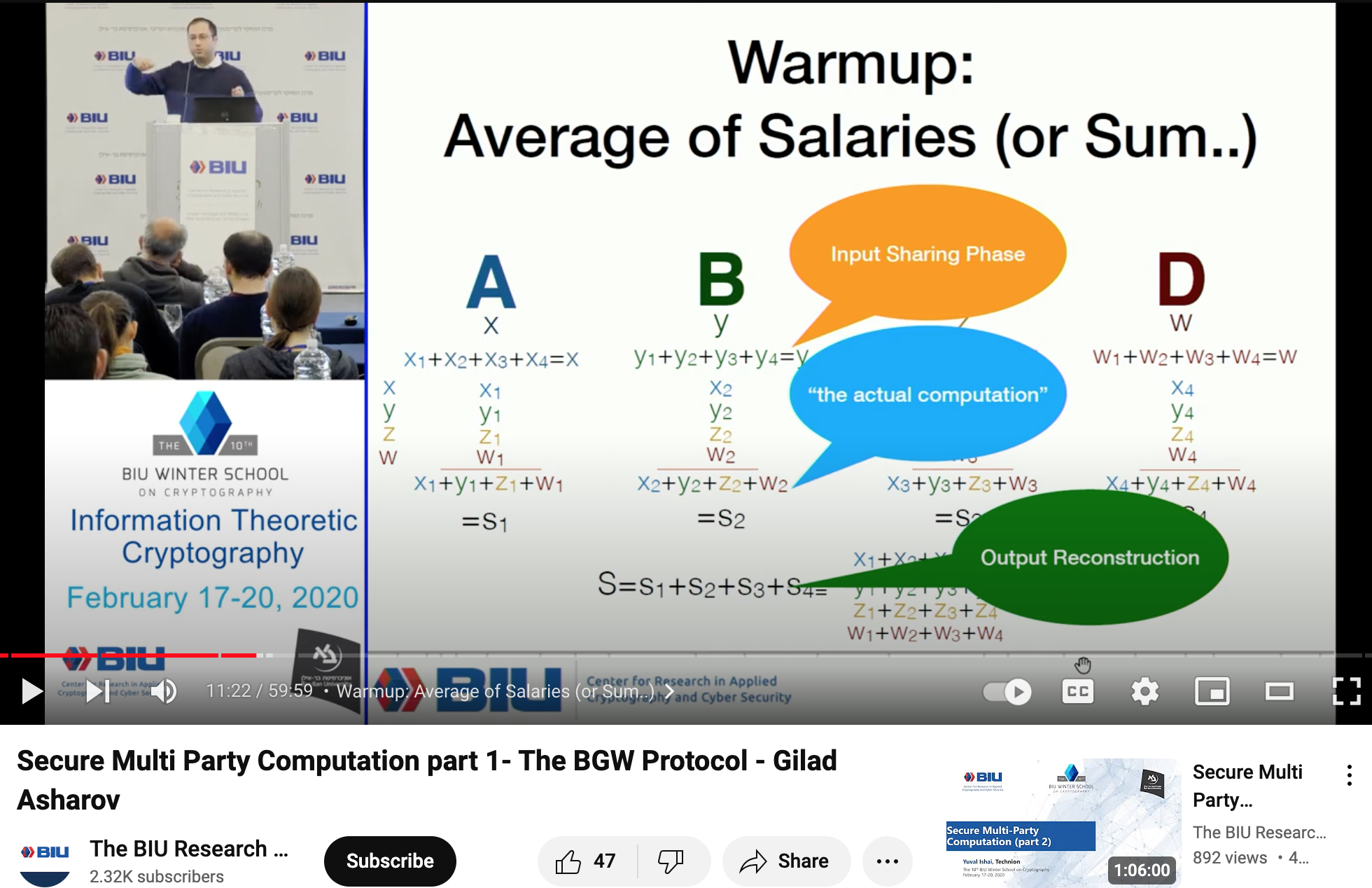
From Two to Three
In the previous Garbled Circuit, we saw how to allow two parties to compute any function without leaking information. (2PC)
If we have 3 parties, how do we compute?
Let’s look at an example: A, B, and C each have private inputs a, b, and c. How can we calculate a + b + c without leaking information?
Custom protocol
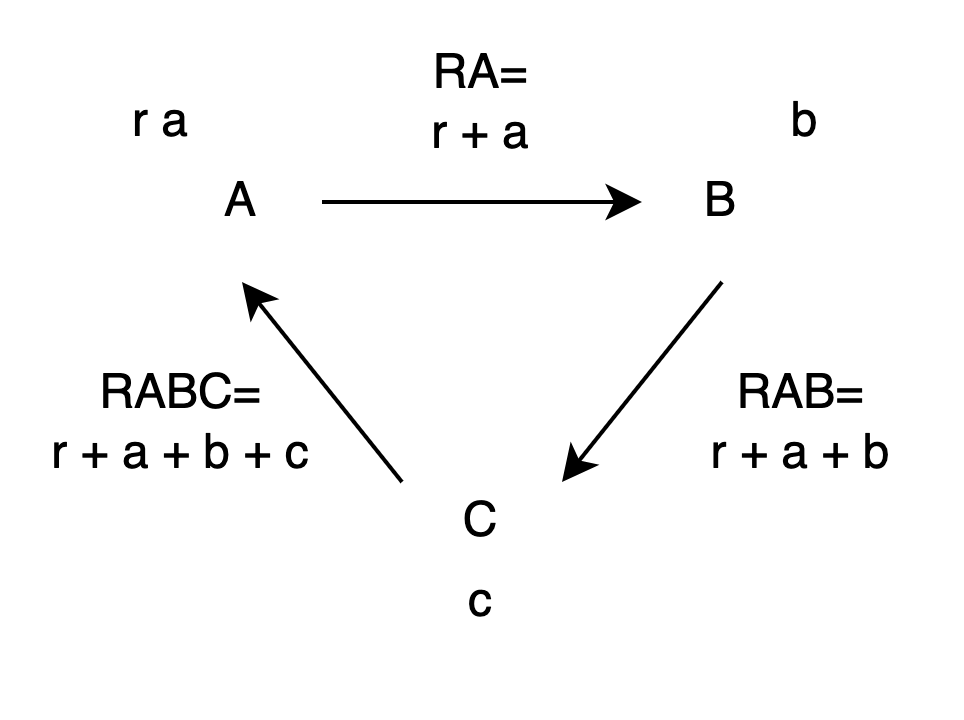
One approach is: A secretly chooses a random number r, adds it to their own number, and secretly sends RA = r + a to B.
B receives RA, adds their own number, and secretly sends RAB = RA + b to C.
C receives RAB, adds their own number, and secretly sends RABC = RAB + c to A.
A receives RABC and calculates RABC - r
RABC - r
= (RAB + c) - r
= (RA + b) + c - r
= (r + a) + b + c - r
= a + b + c
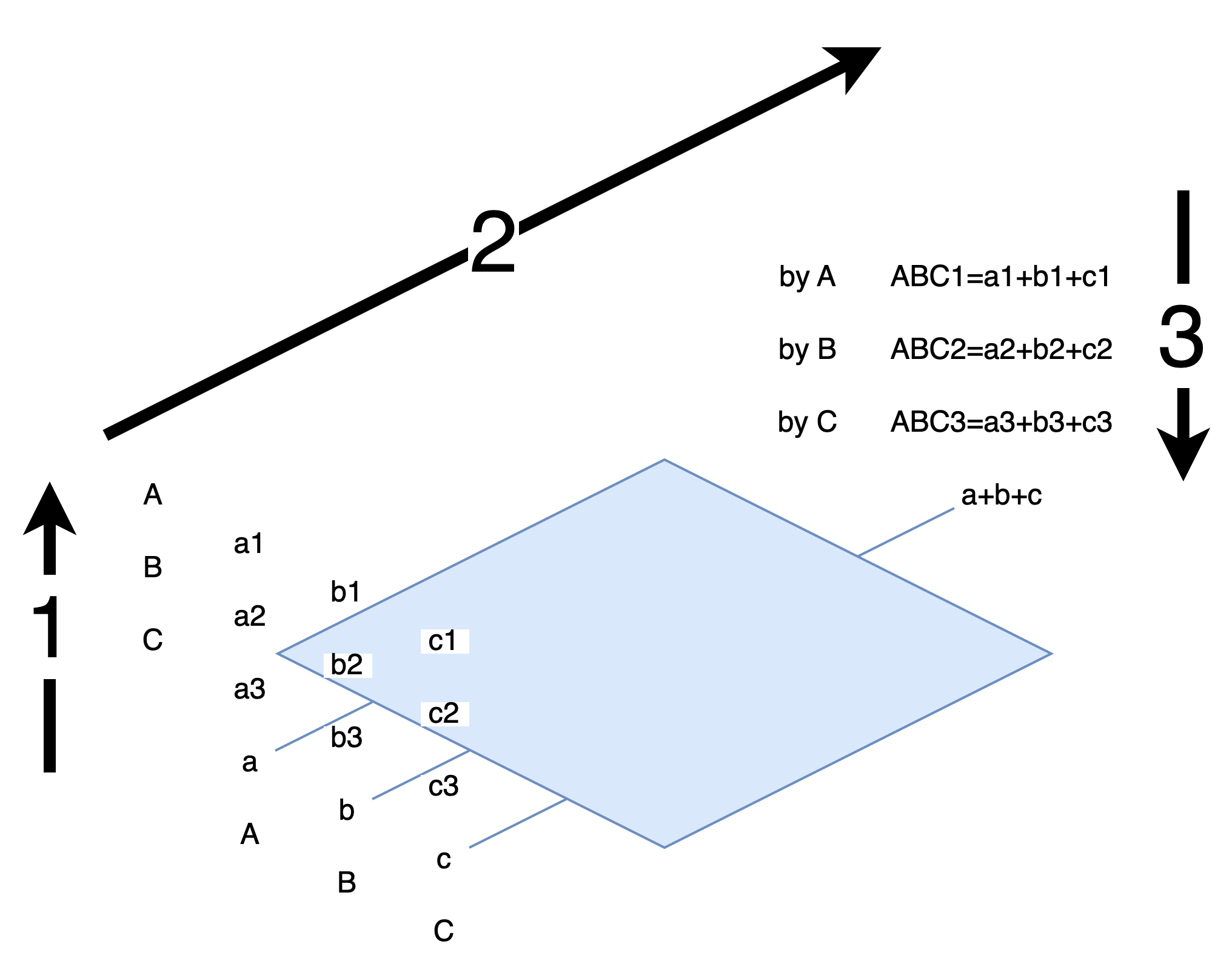
Another custom protocol
Let’s try using additive secret sharing.
Each person secretly splits their input into three parts, such that
a = a1 + a2 + a3
b = b1 + b2 + b3
c = c1 + c2 + c3
A secretly distributes a2 and a3 to B and C.
B secretly distributes b1 and b3 to A and C.
C secretly distributes c1 and c2 to A and B.
A receives b1 and c1, calculates ABC1 = a1 + b1 + c1, and makes it public.
B receives a2 and c2, calculates ABC2 = a2 + b2 + c2, and makes it public.
C receives a3 and b3, calculates ABC3 = a3 + b3 + c3, and makes it public.
Everyone calculates ABC1 + ABC2 + ABC3 to “reconstruct” a + b + c.
(Think about it: if you were A, what information would you have? Is there any way to deduce others’ information?)
In this example, we saw two types of addition.
One is the function to be calculated, which is the addition of a + b + c in the problem itself.
The other is the addition used when splitting/merging during secret sharing.
Later, we’ll see other methods of secret sharing. We’ll also repeatedly see this “split/compute/merge” 3-step approach.
Next, let’s look at a protocol that can handle general problems with more than two parties: GMW.
References:
Secure Multi Party Computation part 1- The BGW Protocol - Gilad Asharov