Point-and-Permute
Bob: Hi Alice.
Alice: Hi Bob.
Bob: Have you seen TBot recently?
Alice: No, I haven’t. What’s up?
Bob: Remember last time when the three of us were discussing Garbled Circuit, and I was the Evaluator? I had to try hard for each row, right?
Alice: Yeah. On average, you had to try 2.5 times for each gate. It wasn’t very convenient.
Bob: Later, I saw an improved method called “point-and-permute”. I wanted to discuss it with you.
Alice: Oh! Let me take a look at the information too! Give me a moment.
(Twelve Seconds Later)
Alice: I’ve finished reading. By the way, you didn’t happen to modify the program too, did you?
Bob: You know me so well! I thought it would be easier to understand with an interactive program, so I modified the one you wrote last time 😅
Remember how we said earlier that we had to try each row one by one? I saw that someone named Beaver suggested that if we add a pointer bit at the end of the label, then when evaluating, we can use the two pointer bits at the end of the two input labels to directly jump to the correct row!
Alice: That’s a bit abstract. Let me try it out…
Garbled Circuit: Point-and-Permute (Evaluator)
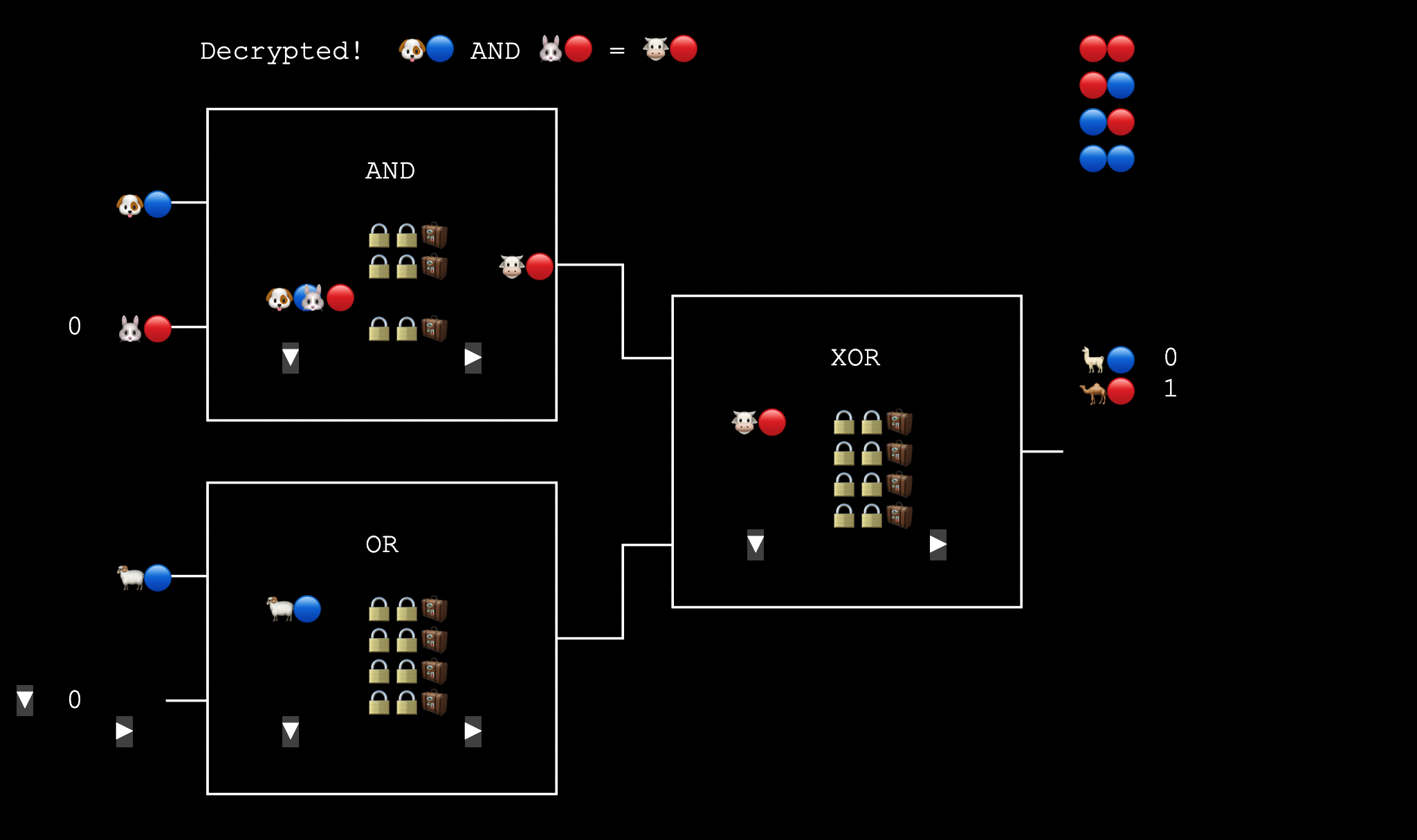
Alice: It works! Just by matching the colors in the top right corner, it’s solved in one go!
So now the table is different from before? Previously it was randomly shuffled, but now it’s arranged according to the colors in the top right corner, right?
Bob: That’s correct. 🔴 means pointer bit = 0, 🔵 means pointer bit = 1.
We sort the input labels according to the pointer bits at the end, 00 01 10 11, and then use them to encrypt the corresponding output label. It’s clearer if we switch to Generator mode.
Garbled Circuit: Point-and-Permute (Generator)
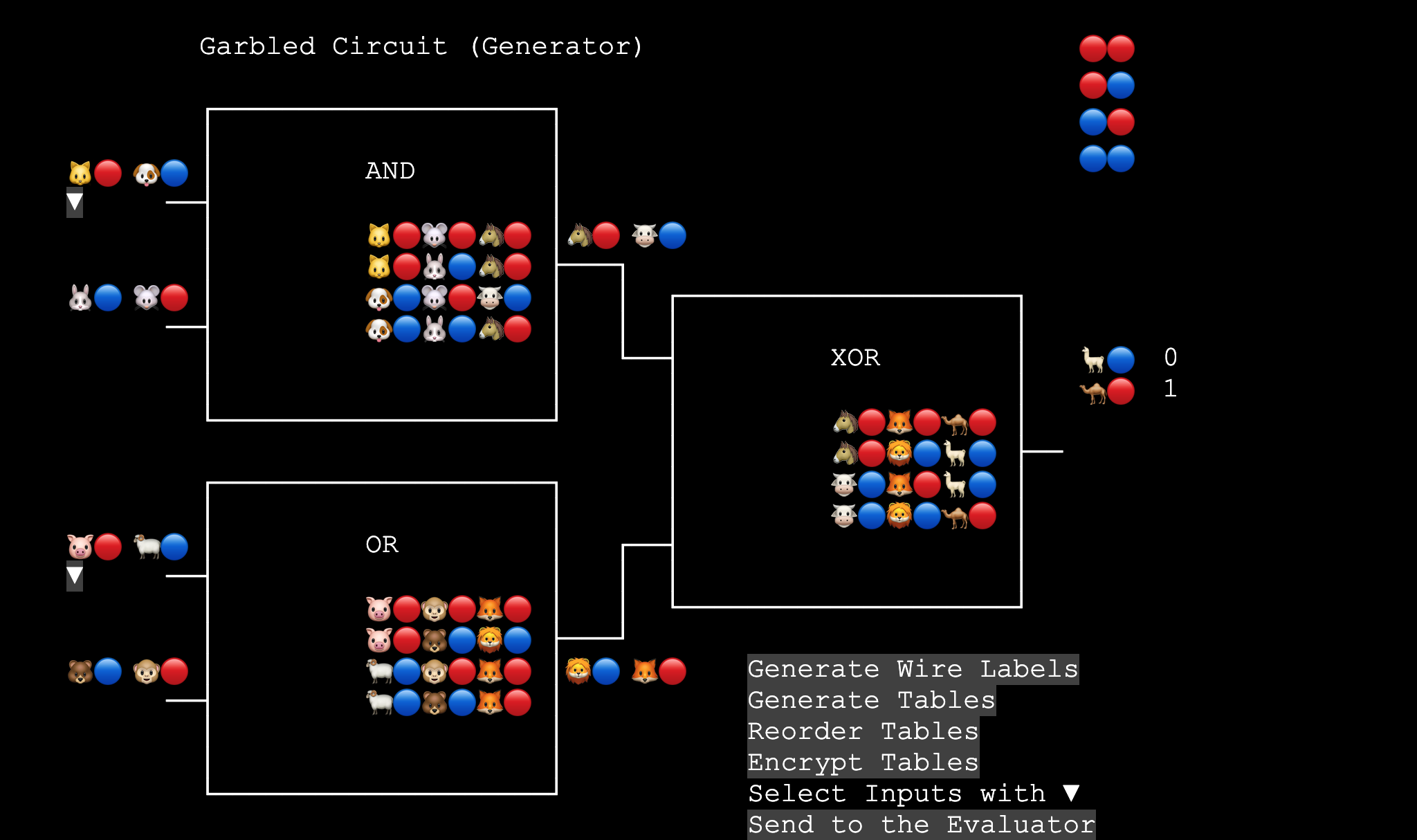
Alice: I pressed “Generate Wire Labels” several times. Before, the first wire only had 🐱🐶 or 🐶🐱, but now it can be followed by 🔴🔵 or 🔵🔴, so there should be these four combinations:
0 1
🐱🔴🐶🔵 🐱=0 🐶=1
🐱🔵🐶🔴 🐱=0 🐶=1
🐶🔴🐱🔵 🐶=0 🐱=1
🐶🔵🐱🔴 🐶=0 🐱=1
Bob: Mm-hmm. If I’m the Evaluator and I get 🐱🔴, although I see more than before with the 🔴, because how 🐱🐶 and 🔴🔵 are paired is completely random, I still can’t tell if 🐱 is 0 or 1. After all, both of these cases are possible:
0 1
🐱🔴 _ _ 🐱 = 0
_ _ _ _
_ _ _ _
_ _ 🐱🔴 🐱 = 1
Alice: I pressed “Generate Tables” again. If we cover up the colors here and only look at the animals, it’s just a regular truth table. The AND gate’s output is still “3 / 1”, and the OR gate’s output is still “1 / 3”.
Bob: The main difference is in the next step, “Reorder Tables”. As you mentioned earlier, before we randomly shuffled the rows, but now we sort the rows according to the colors of the input labels. So the color order is the same as in the top right corner.
🔴🔴
🔴🔵
🔵🔴
🔵🔵
Alice: We could also think of it this way: before, we used coin flips to decide whether two things would be shuffled into AB or BA. Now, we first flip coins to decide the color arrangement, stick the colors on A and B, and then use the colors to sort A and B, which indirectly shuffles A and B.
Bob: Indeed, these colors are simply for sorting. And because which color is stuck on what is randomly decided, even after sorting by color, it still doesn’t reveal the original information.
Alice: The next part is very similar to before, right? Use two input labels to encrypt the output label. Only one of the four outputs will be decrypted.
The difference is that now the table is sorted by the colors of the input labels, so when the evaluator gets there, they can directly go to the row pointed to by the colors of the two input labels, and decrypt it in one go! That’s great!
Bob: And the decrypted output label also has a color, so for the next gate, it can also be decrypted in one go.
Alice: The one after that can also be decrypted in one go.
Bob: And the one after that… Okay, let’s stop here for today! Thank you very much for discussing this with me!
Alice: Thank you too. See you next time!
(Fin)