淺談 Garbled Circult 與 Oblivious Transfer
Alice, Bob: Hi TBot.
TBot: Hi Alice, Bob.
Alice: Bob 和我手上各有一個秘密的數字. 你可以我們比大小嗎? 不可以把數字洩漏出去喔.
TBot: 好的. 那 Alice 你的數字是多少?
Alice: 我的數字是 xx (在 TBot 耳邊說)
TBot: 收到. 那 Bob 你呢?
Bob: 我的數字是 yy (在 TBot 耳邊說)
TBot: 收到. 經過我的比較, 數字比較大的是… Alice!
Alice: 耶!
(幾天後)
Bob: Hi TBot.
TBot: Hi Bob, Alice.
Bob: 聽說你可能有一陣子會不在? 這樣我們要找誰幫忙比大小呢?
TBot: 讓我查一下資料…
TBot: 有了. 大概快 40 年前, 有一個叫 “Yao” 的人, 發明了 "Garbled Circuit". 不光是比大小, 只要你們把想計算的 function 表達成 boolean circuit, 就可以用 garbled circuit 的方式來計算了.
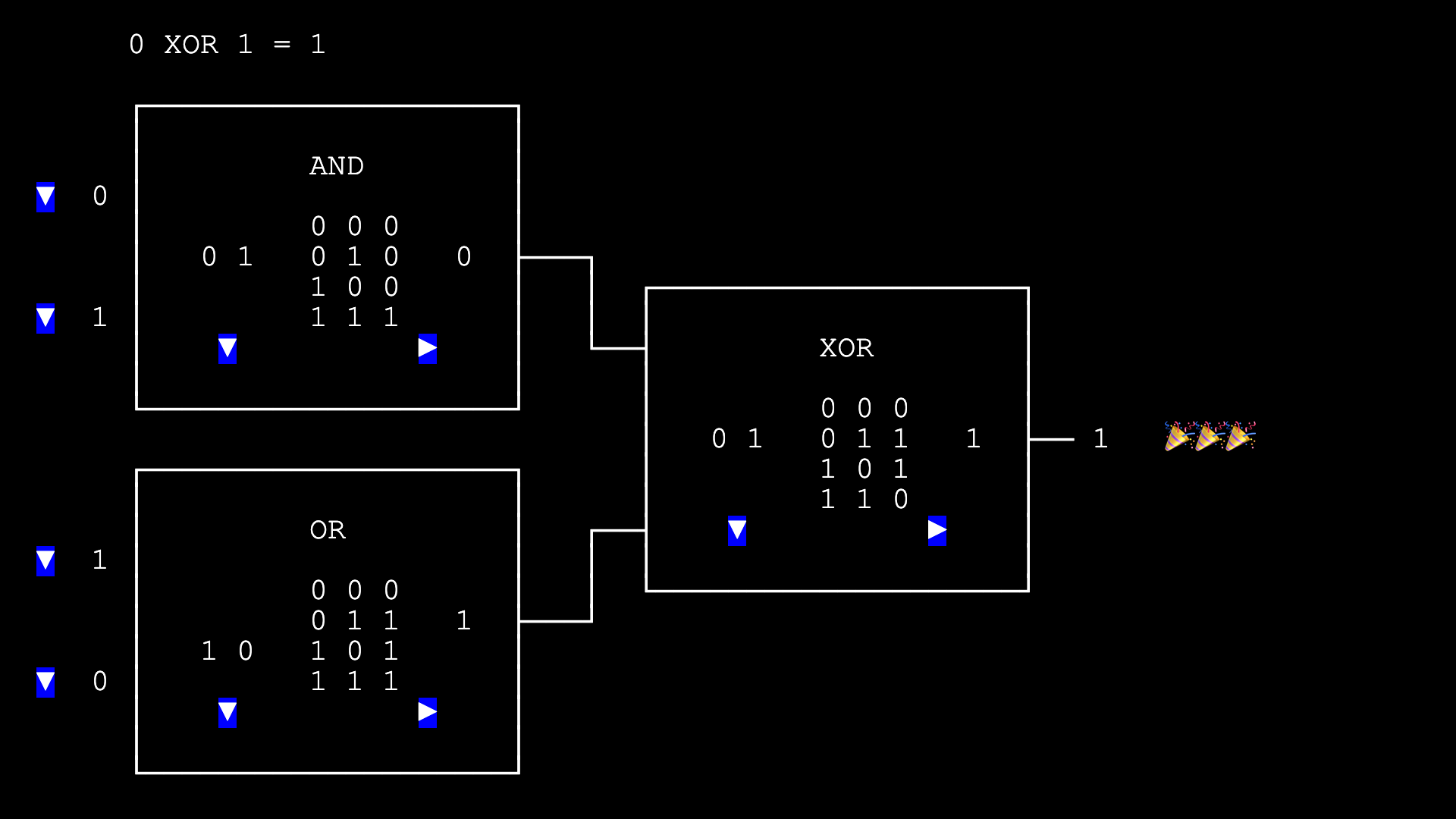
先看一下普通的 boolean circuit. Bob, 你可以不要用心算, 而是用這個網頁來 evaluate (0 AND 1) XOR (1 OR 0) 嗎?
Bob: 答案是 1. 然後呢?
TBot: Garbled circuit 的想法是, 每一條 wire 上面如果傳的不是 0 或 1, 而是看不懂的 label 的話, 那就可以在不知道對方秘密的狀況下做計算了.
比方說, 如果把第一個 AND Gate 先換成這樣, 能看得出 label 代表的值嗎?
AND gate
a b c a b c
0 0 0 🐱 🐭 🐮
0 1 0 🐱 🐰 🐮
1 0 0 🐶 🐭 🐮
1 1 1 🐶 🐰 🐴
Bob: 嗯… 雖然現在表面上不是 0 1 了, 但這只是文字代換吧? 從位置來看, 🐱 🐶 應該是 wire a 的 0 1, 🐭 🐰 應該是 wire b 的 0 1 吧? 這樣有保密嗎?
TBot: 的確沒有保密. 那如果把四個 row shuffle 過呢? 你們還看得出來嗎?
AND gate
a b c
🐱 🐰 🐮
🐶 🐰 🐴
🐶 🐭 🐮
🐱 🐭 🐮
Alice: 從 a b 的確看不出來. 但因為這是個 AND gate, 所以從 c 來看, 只出現一次的 🐴 應該是 1. 那 🐶 🐰 就是 a b 的 1 了.
TBot: 沒錯! 那如果只顯示給定 input 的那個 row 呢?
AND gate
a b c
x x x
x x x
🐶 🐭 🐮
x x x
Alice: 這樣應該保密了, 沒辦法猜出這些 label 是 0 還是 1.
Bob: 嗯嗯. 而且知道超過一個 output 可能就危險了. 因為 AND gate 只有一個 output 是 1, 像下面這樣就會被看出 🐮 是 0 了.
AND gate
a b c
x x x
x x x
x x 🐮
x x 🐮
TBot: 你們的觀察很深入! 當拿到兩個 wire 的 input label 的時候, 我們必須能算出正確且唯一的 output label. 其他 output label 都必須隱藏起來.
Bob, 你可以再當一次 Evaluator 來算看看 (? AND 1) XOR (? OR 0) 嗎?
Bob: 這兩個 “?” 是 Alice 的 input 嗎?
TBot: 是的. Alice 會用 label 把她的兩個 input 傳給你. 而 1 和 0 是你的兩個 input.
Bob: 算完了, 答案是 1. 這就是稍早說的: 用保密的 label 來計算嗎?
TBot: 是的! 雖然你不知道每個 label 代表的是 0 還是 1, 但是每一步你都算出了正確的 label.
Bob: 原本的 truth table 在這邊也變成四個上鎖的箱子了.
TBot: 普通的 boolean circuit 有一個明文的 truth table 讓我們做計算.
而 garbled circuit 中, 為了算出唯一一個 output label 且隱藏其他的 labels, Yao 用了一個技巧, 也就是 用兩個 input labels 當成 keys 去 encrypt 對應的 output label.
而計算時則用兩個 input labels 去逐一試著 decrypt, 唯一能 decrypt 出來的那個就是對的 output label.
所以 gate 的 table 變成四個值
🔒🔒🧳 = Encrypt(input label, input label, output label)
🔒🔒🧳 = Encrypt(input label, input label, output label)
🔒🔒🧳 = Encrypt(input label, input label, output label)
🔒🔒🧳 = Encrypt(input label, input label, output label)
舉例來說, 如果 shuffle 後的 table 長成這樣:
AND gate
a b c
🐱 🐰 🐮
🐶 🐰 🐴
🐶 🐭 🐮
🐱 🐭 🐮
那加密後的 table 就只有下面四個值:
i i o
🔒🔒🧳 = Encrypt(🐱, 🐰, 🐮)
🔒🔒🧳 = Encrypt(🐶, 🐰, 🐴)
🔒🔒🧳 = Encrypt(🐶, 🐭, 🐮)
🔒🔒🧳 = Encrypt(🐱, 🐭, 🐮)
Bob: 也就是說, 如果我有這個 gate 的 input 🐶 和 🐭, 那我只能唯一 decrypt 出第三個 row 的 🐮, 而且也看不到 🐴 是嗎?
TBot: 沒錯! 所以你只能取得唯一的 output 🐮. 無法推測出 🐮 到底是 0 還是 1, 也推測不出 🐶 和 🐭 是 0 還是 1.
Bob: 了解. 操作過上面的 circuit 後, 我大概知道怎麼算了. 但是你不在的時候, 我們要去哪裡取得這種編碼過的 circuit 呢?
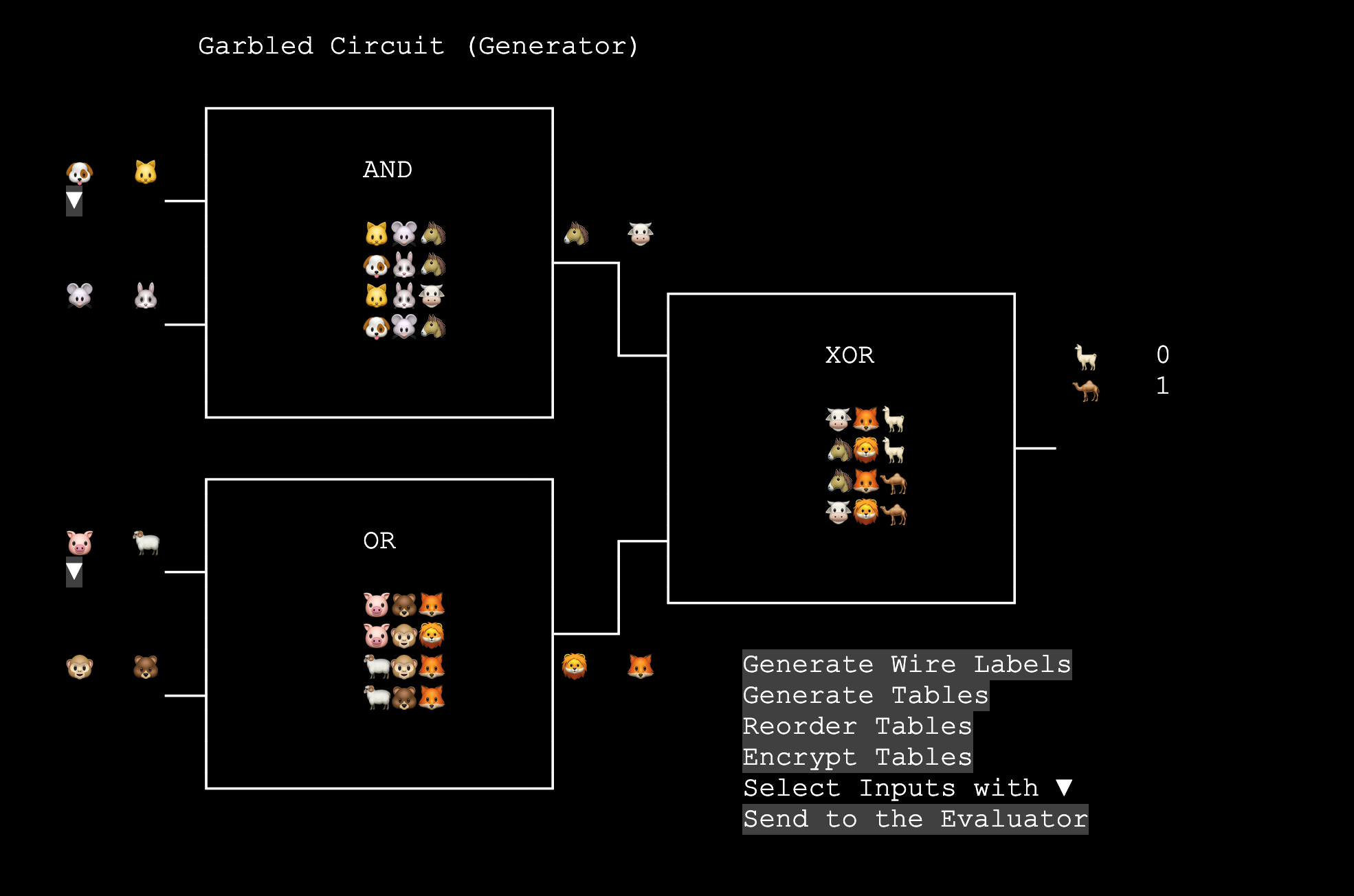
TBot: 這就是 Generator 的工作了. Generator 會把每個 wire 的 0 和 1 編成對應的 labels. 再把加密過的 tables 和 input labels 傳給你計算. Alice 你可以試看看嗎?
Alice: 好. 不過可以等久一點嗎?
TBot: OK.
(Twelve Seconds Later)
Alice: 從前面的討論來看, 我把 TBot 給的網頁改了一下. 做為 Generator, 我想我應該要
- 把每個 wire 的 0 1 都各取一個 label
- 把 truth table 的 0 1 也都換成 label
- 把 table 的四個 row shuffle 過
- 把四個 output 用對應的兩個 input 加密, 這樣才能讓 Bob 解出唯一一個 output 來往下走
- 把加密過的結果給 Bob
- 我的輸入換成 labels 也給 Bob
- 最後結果的 wire 的 labels 也給 Bob
Alice: 大概是這些吧. 但如果 TBot 不在的話, 還少了個功能…
Bob: 我拿到你的 input 的 label 了. 可是你還沒給我我的 input 的 label.
Alice: 嗯嗯. 我不知道你的 input 是 0 還是 1, 所以不知道要拿哪個 label 給你. 但我又不能把 0 1 兩個 label 都給你讓你自己挑, 因為這樣你手上的資訊就能解開不只一個 output 了.
Bob: 但我也不能和你說 “我的 input 是 1, 請給我代表 1 的 label”, 這樣直接就洩密了.
Alice: 所以我們要想個方法, 讓你只拿到兩個 label 中你挑的那一個, 而我卻不知道你實際上挑了哪個.
TBot: 這個問題很有趣, 它就叫…
Alice, Bob: 等一下!
(一陣討論)
Bob: 或許你可以把兩個 label 裝兩箱送給我, 而讓我只開的了其中一個箱子.
Alice: 但我不知道你想開哪個, 所以箱子應該由你準備, 由你決定哪個是可以開的.
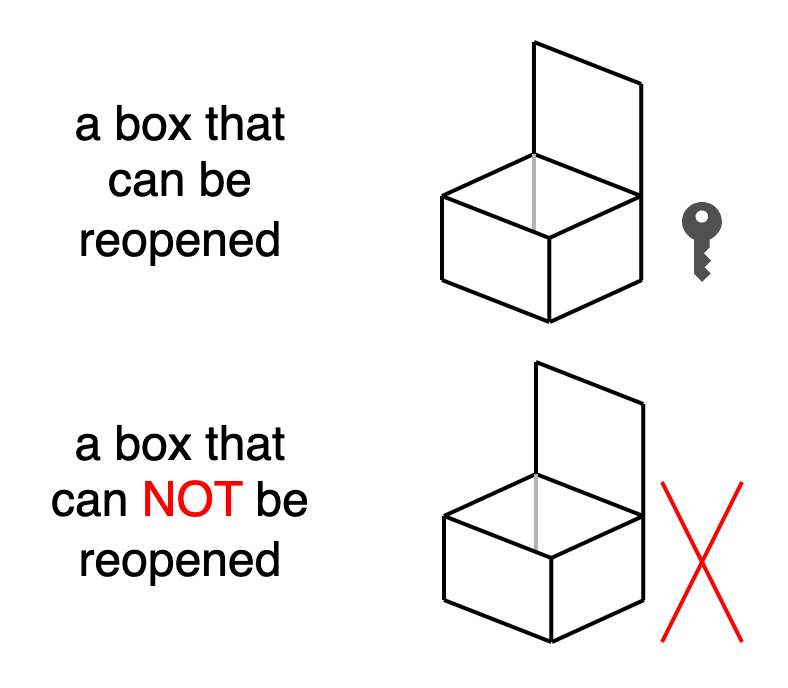
Bob: 那由我準備兩個箱子, 一個是關起來以後打的開的, 一個是關起來以後打不開的. 把兩個箱子開著送給你.
Alice: 這兩個箱子從外觀我看不出哪個能再開, 所以我不知道你想開的是哪個. 我把 0 1 兩個 label 依序放進去, 再關起來送給你.
Bob: 如果當初我想拿 label 0, 我就會在前面放可以再打開的箱子. 這樣你送來我也只能開出 label 0.
Alice: 我也相信你是誠實的. 不會拿兩個都能再開的箱子給我.
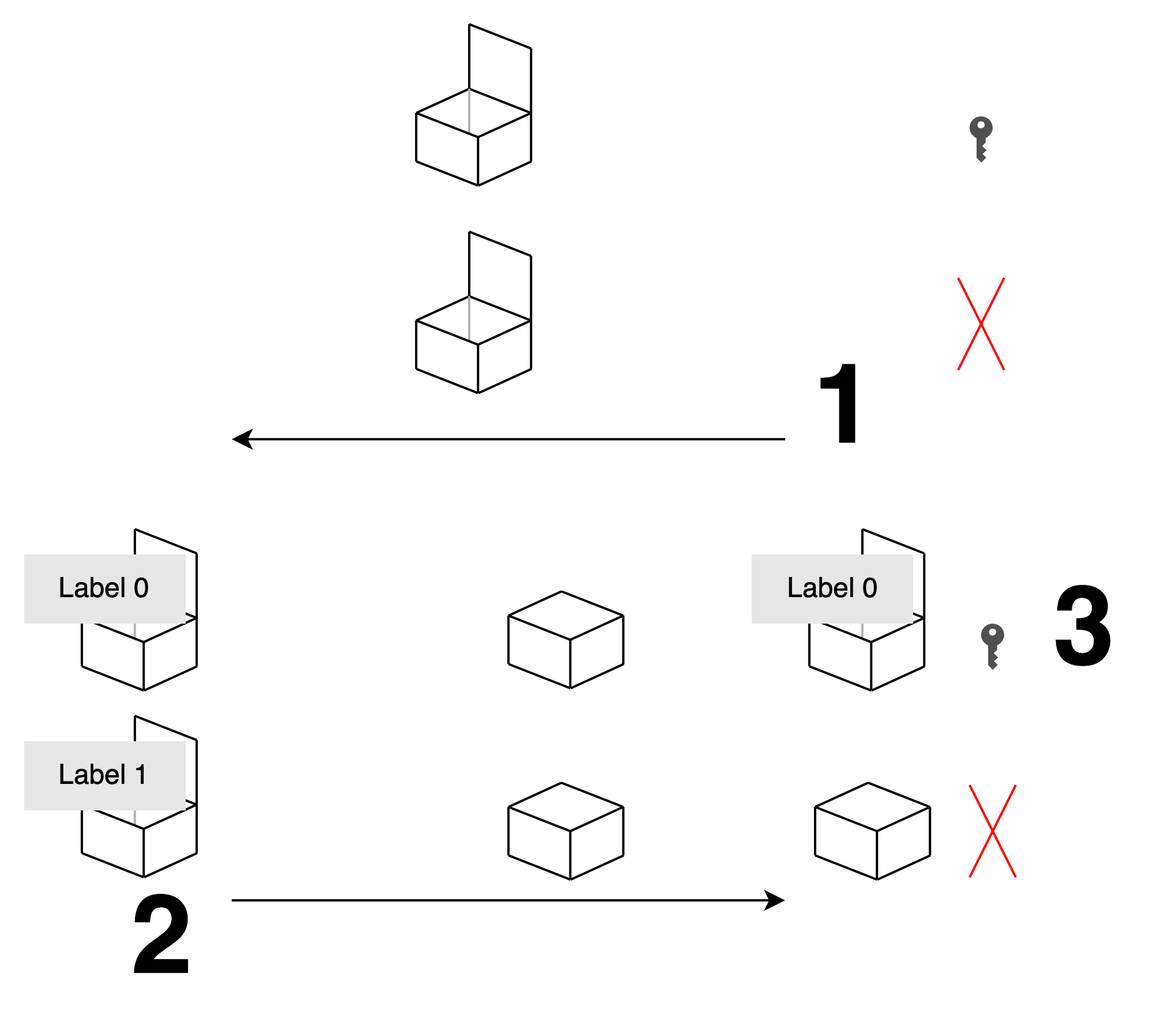
Bob: 看來這樣可行. 不過用實體的箱子比較麻煩, 能不能用數位的方式呢?
TBot: 這個問題有個解法, 就是…
Alice, Bob: 再等一下!
(一陣討論)
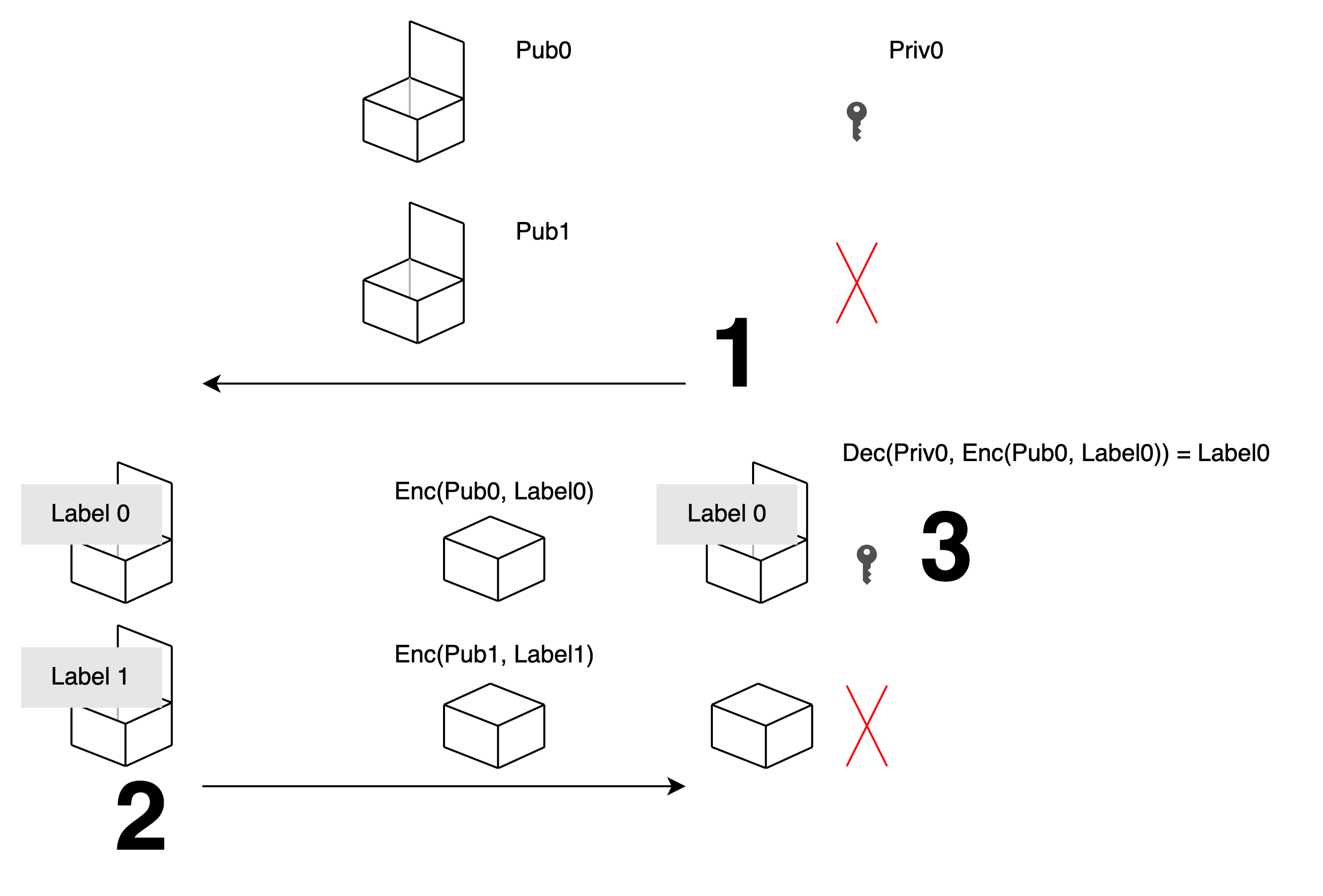
Alice: 如果裝箱想成是加密, 打開想成是解密. 你可以生成一對 public key 和 private key 來代表可以再開的箱子.
Bob: 我把那個 public key 送給你. 你用它來加密 label 以後送給我, 我就能用 private key 解開.
Alice: 我們還需要一個打不開的箱子.
Bob: 那我再單獨在 public key 的數字中亂挑一個出來, 而我不知道它對應的 private key, 這樣就解不開了.
Alice: 這樣很好. 就算有人在你旁邊偷看, 因為你沒有產出 private key, 所以我用這個 public key 加密以後, 偷看的人也解不開.
Bob: 也就是最一開始, 我生兩個像 public key 的數字送給你, 其中一個我知道 private key.
Alice: 我用這兩個看起來是 public key 的數字分別加密兩個 label 送給你, 但我不會知道哪一個你解的開.
Bob: 我解開有 private key 對應的的那個 label, 另外一個我解不開, 不會洩密. 就這樣.
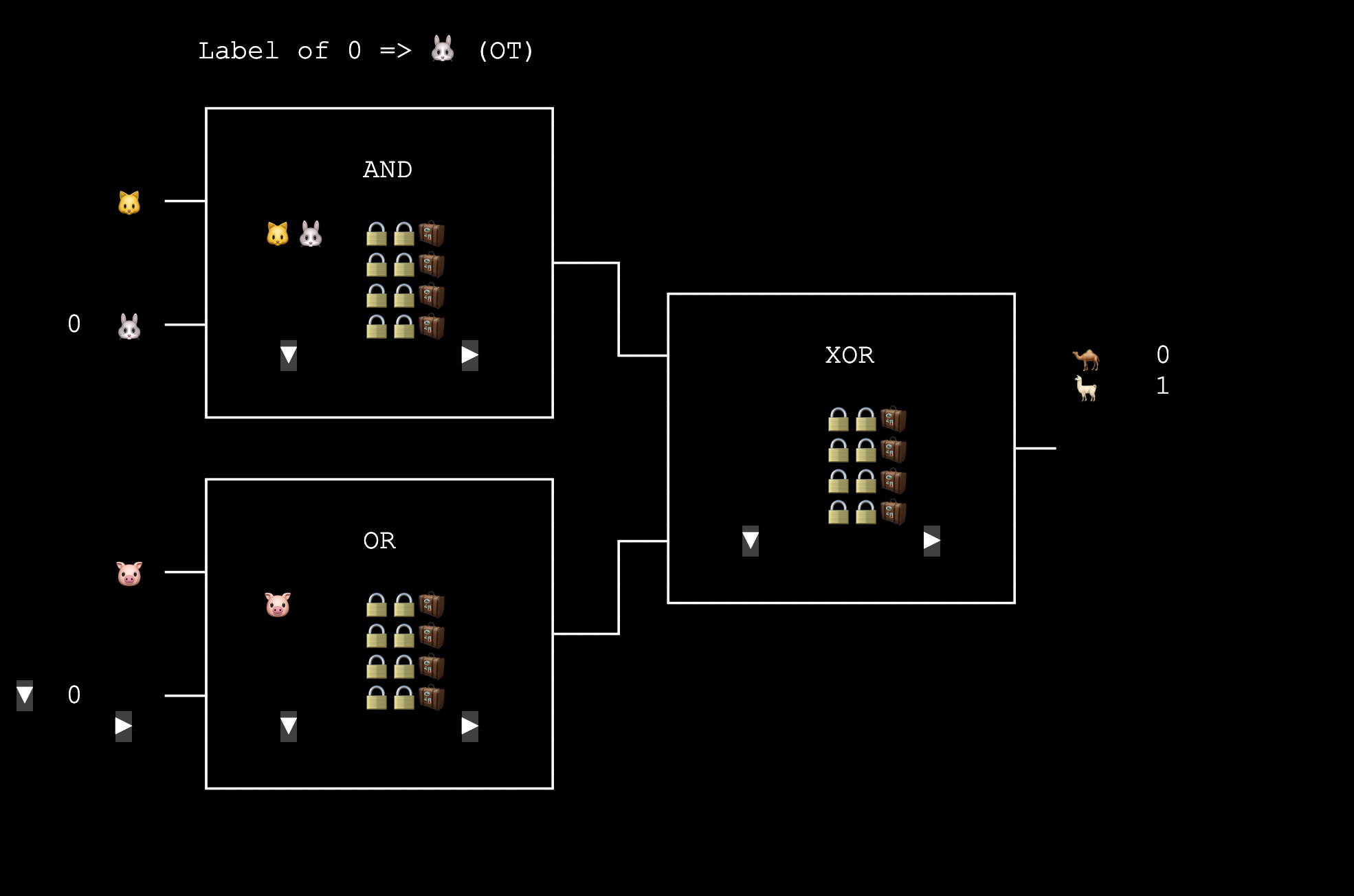
TBot: 看起來你們有解法了. 為了方便找資料, 我還是講一下名字好了. Bob, 還記得之前你當 Evaluator 取得自己 input label 的時候, 系統顯示什麼訊息嗎?
Bob: 有出現 “Label of 0 => 🐰 (OT)” 這樣的訊息.
TBot: 這種 “不知道對方收到什麼” 的傳送方式就叫做 "Oblivious Transfer" (OT).
OT 有很多變種, 剛剛這種有人叫他 “chosen one-out-of-two OT”: 由 Receiver 選 0 或 1, 而由 Sender 提供兩筆資料. Sender 不會知道 Receiver 選的是 0 還是 1, Receiver 也無法讀到另一筆沒選的資料.
如果不會和其他 OT 弄混的話, 也常有人寫成 “one-out-of-two OT”, “$\binom{2}{1}$ OT”, 或直接只寫 “OT”.
Bob: 要是 TBot 你一直都在, 我們就把兩筆資料和 0 1 都給你, 你再把選到那筆給我就好了.
Alice: 要是 TBot 一直都在, 我們也不需要 Garbled Circuit 了.
TBot: 那個能讓你們一直 trust 的我, 大概只存在理想世界中吧? 啊哈哈哈哈.
Alice: 啊哈哈哈哈
Bob: 啊哈哈哈哈
(Fin)